4-manifolds: 1-connected
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Any finitely presentable group may occur as the fundamental group of a smooth closed 4-manifold. On the other hand, the class of simply connected (topological or smooth) 4-manifolds still appears to be quite rich, so it appears reasonable to consider the classification of simply connected 4-manifolds in particular.
It appears that the intersection form is the main algebro-topological invariant of simply-connected 4-manifolds.
Technical remark: When we mention the term 4-manifold without the explicit mention of topological or smooth we shall mean the larger class of topological 4-manifolds.
2 Construction and examples, their intersection forms
...
2.1 First examples
The first examples that come to one's mind are the 4-sphere 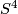 , the complex projective space
, the complex projective space 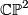 , the complex projective space with its opposite (non-complex) orientation
, the complex projective space with its opposite (non-complex) orientation 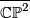 , the product
, the product 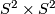 , various connected sums of these, and in particular
, various connected sums of these, and in particular 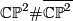 .
.
The intersection form of the 4-sphere is the "empty form" of rank 0. The intersection forms of the others are given by
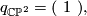
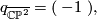
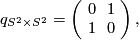
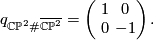
The manifolds 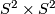 and
and 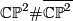 both have indefinite intersection forms of same rank and signature, but of different type. Therefore they are not homotopy-equvialent.
both have indefinite intersection forms of same rank and signature, but of different type. Therefore they are not homotopy-equvialent.
2.2 Hypersurfaces in CP3
For an integer 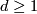 we define a subset
we define a subset 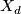 of
of 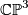 by the formula
by the formula
![\displaystyle S_d = \{ X_0^d + X_1^d + X_2^d + X_3^d = 0 | [X_0:X_1:X_2:X_3] \in \mathbb{CP}^3 \} .](/images/math/2/9/e/29e4e39ed8f3b8a56332f16a391355a5.png)
It is easy to check that in each chart of 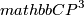 the
the 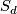 is cut out transversally by the homogeneous polynomial of degree
is cut out transversally by the homogeneous polynomial of degree  . This is a special case of a complete intersection.
. This is a special case of a complete intersection.
2.3 Elliptic surfaces
2.4 Branched coverings
2.5 The E8 manifold
3 Invariants
...
4 Topological classification
...
5 Non-existence results for smooth 4-manifolds
...
6 The Seiberg-Witten invariants
...
7 Failure of the h-cobordism theorem
...
8 Further discussion
...