4-manifolds: 1-connected
| Line 33: | Line 33: | ||
The intersection form of the 4-sphere is the "empty form" of rank 0. The intersection forms of the others are given by | The intersection form of the 4-sphere is the "empty form" of rank 0. The intersection forms of the others are given by | ||
$$ | $$ | ||
| − | q_{\mathbb{CP}^2} | + | q_{\mathbb{CP}^2} = ( \ 1 \ ) , |
| − | q_{\overline{\mathbb{CP}^2}} = ( \, -1 \ ) | + | $$ |
| − | + | $$ | |
| − | q_{S^2 \times S^2} = | + | q_{\overline{\mathbb{CP}^2}} = ( \, -1 \ ) , |
| + | $$ | ||
| + | $$ | ||
| + | q_{S^2 \times S^2} = \begin{pmatrix} \ 0 \ & \ 1 \ \\ 1 & 0 \end{pmatrix} , | ||
| + | $$ | ||
| + | $$ | ||
| + | q_{\mathbb{CP}^2 \# \overline{\mathbb{CP}^2}} = \begin{pmatrix} \ 1 \ & \ 0 \ \\ 0 & -1 \end{pmatrix} . | ||
$$ | $$ | ||
Revision as of 11:59, 8 June 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Any finitely presentable group may occur as the fundamental group of a smooth closed 4-manifold. On the other hand, the class of simply connected (topological or smooth) 4-manifolds still appears to be quite rich, so it appears reasonable to consider the classification of simply connected 4-manifolds in particular.
It appears that the intersection form is the main algebro-topological invariant of simply-connected 4-manifolds.
Technical remark: When we mention the term 4-manifold without the explicit mention of topological or smooth we shall mean the larger class of topological 4-manifolds.
2 Construction and examples, their intersection forms
...
2.1 First examples
The first examples that come to one's mind are the 4-sphere  , the complex projective space
, the complex projective space 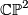 , the complex projective space with its opposite (non-complex) orientation
, the complex projective space with its opposite (non-complex) orientation 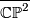 , the product
, the product 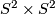 , various connected sums of these, and in particular
, various connected sums of these, and in particular 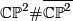 .
.
The intersection form of the 4-sphere is the "empty form" of rank 0. The intersection forms of the others are given by
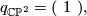
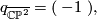
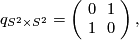
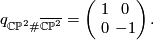
2.2 Hypersurfaces in $\mathbb{CP}^3$
2.3 Elliptic surfaces
2.4 Branched coverings
2.5 The $E_8$ manifold
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...