3-manifolds in 6-space
| This page has been accepted for publication in the Bulletin of the Manifold Atlas. |
For notation and conventions see high codimension embeddings.
Contents |
1 The Haefliger trefoil knot
Let us construct a smooth embedding 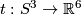 (which is a generator of
(which is a generator of 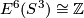 ) [Haefliger1962], 4.1. A miraculous property of this embedding is that it is not
) [Haefliger1962], 4.1. A miraculous property of this embedding is that it is not 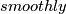 isotopic to the standard embedding, but is
isotopic to the standard embedding, but is 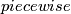
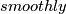 isotopic to the standard embedding.
isotopic to the standard embedding.
Denote coordinates in 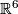 by
by 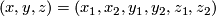 . The higher-dimensional trefoil knot
. The higher-dimensional trefoil knot  is obtained by joining
with two tubes the higher-dimensional
is obtained by joining
with two tubes the higher-dimensional 
 , i.e. the three spheres given by the following three systems of equations:
, i.e. the three spheres given by the following three systems of equations:
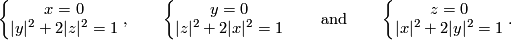
See Figures 3.5 and 3.6 of [Skopenkov2006].
2 The Hopf construction of an embedding 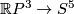
Represent 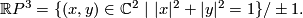 Define
Define
![\displaystyle Ho:\Rr P^3\to S^5\subset\Cc^3\quad\text{by}\quad Ho[(x,y)]=(x^2,2xy,y^2).](/images/math/d/7/a/d7a26b0af78cfc97ff3048bf1296424e.png)
It is easy to check that 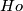 is an embedding. (The image of this embedding is given by the equations
is an embedding. (The image of this embedding is given by the equations 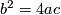 ,
, 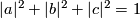 .)
.)
It would be interesting to obtain an explicit construction of an embedding 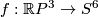 which is not isotopic to the composition of the Hopf embedding with the standard inclusion
which is not isotopic to the composition of the Hopf embedding with the standard inclusion 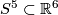 . (Such an embedding
. (Such an embedding  is unique up to PL isotopy by classification just below the stable range.)
is unique up to PL isotopy by classification just below the stable range.)
3 Algebraic embeddings from the theory of integrable systems
Some 3-manifolds appear in the theory of integrable systems together with their embeddings into 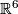 (given by a system of algebraic equations) [Bolsinov&Fomenko2004], Chapter 14. E.g. the following system of equations corresponds to the Euler integrability case:
(given by a system of algebraic equations) [Bolsinov&Fomenko2004], Chapter 14. E.g. the following system of equations corresponds to the Euler integrability case:
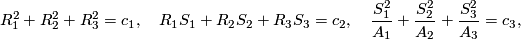
where 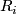 and
and 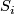 are variables while
are variables while 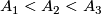 and
and 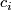 are constants.
This defines embeddings of
are constants.
This defines embeddings of  ,
, 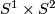 or
or 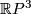 into
into 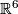 .
.
4 References
- [Bolsinov&Fomenko2004] A. V. Bolsinov and A. T. Fomenko, Integrable Hamiltonian systems, Chapman \& Hall/CRC, Boca Raton, FL, 2004. MR2036760 (2004j:37106) Zbl 1056.37075
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 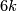 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
|
This page has not been refereed. The information given here might be incomplete or provisional. |