3-manifolds in 6-space
| Line 1: | Line 1: | ||
| − | For notation and conventions see [[High_codimension_embeddings|high codimension embeddings]]. | + | For notation and conventions throughout this page see [[High_codimension_embeddings|high codimension embeddings]]. |
== Examples == | == Examples == | ||
| − | |||
=== The Haefliger trefoil knot === | === The Haefliger trefoil knot === | ||
<wikitex>; | <wikitex>; | ||
| Line 37: | Line 36: | ||
== Invariants == | == Invariants == | ||
<wikitex>; | <wikitex>; | ||
| − | For notation and conventions see [[High_codimension_embeddings|high codimension embeddings]]. For classification theorem involving the Kreck invariant see [[Classification_of_embeddings_of_3-manifolds_in_the_6-space|classification of embeddings of 3-manifolds in the 6-space]]. | + | <!--For notation and conventions see [[High_codimension_embeddings|high codimension embeddings]]. For classification theorem involving the Kreck invariant see [[Classification_of_embeddings_of_3-manifolds_in_the_6-space|classification of embeddings of 3-manifolds in the 6-space]]. --> |
| − | Let $N$ be a closed connected orientable 3-manifold. | + | Let $N$ be a closed connected orientable 3-manifold. An orientation-preserving diffeomorphism $\varphi:\partial C_f\to\partial C_{f'}$ such that $\nu_f=\nu_{f'}\varphi$ is simply called an $isomorphism$. For an isomorphism $\varphi$ denote |
| − | + | ||
| − | An orientation-preserving diffeomorphism $\varphi:\partial C_f\to\partial C_{f'}$ such that $\nu_f=\nu_{f'}\varphi$ is simply called an $isomorphism$. For an isomorphism $\varphi$ denote | + | |
$$M=M_\varphi:=C_f\cup_\varphi(-C_{f'}).$$ | $$M=M_\varphi:=C_f\cup_\varphi(-C_{f'}).$$ | ||
An isomorphism $\varphi:\partial C_f\to\partial C_{f'}$ is called $spin$, if $\varphi$ over $N_0$ is defined by an isotopy between the restrictions of $f$ and $f'$ to $N_0$. A spin isomorphism exists because the restrictions to $N_0$ of $f$ and $f'$ are isotopic (see the definition of the Whitney invariant in [[Classification_just_below_the_stable_range|classification just below the stable range]]) and because $\pi_2(SO_3)=0$. If $\varphi$ is a spin isomorphism, then $M_\varphi$ is spin \cite{Skopenkov2008}, Spin Lemma. | An isomorphism $\varphi:\partial C_f\to\partial C_{f'}$ is called $spin$, if $\varphi$ over $N_0$ is defined by an isotopy between the restrictions of $f$ and $f'$ to $N_0$. A spin isomorphism exists because the restrictions to $N_0$ of $f$ and $f'$ are isotopic (see the definition of the Whitney invariant in [[Classification_just_below_the_stable_range|classification just below the stable range]]) and because $\pi_2(SO_3)=0$. If $\varphi$ is a spin isomorphism, then $M_\varphi$ is spin \cite{Skopenkov2008}, Spin Lemma. | ||
| Line 57: | Line 54: | ||
(Since $H_4(Q)\cong[Q,\Cc P^\infty]$, there is a closed connected oriented 4-submanifold $X\subset Q$ representing the class $x$. Then $3\sigma(X)=p_1(X)=xPDp_1(Q)-x^3=3\sigma_x(Q)$ by \cite{Hirzebruch1966}, end of 9.2 or else by \cite{Skopenkov2008}, Submanifold Lemma.) | (Since $H_4(Q)\cong[Q,\Cc P^\infty]$, there is a closed connected oriented 4-submanifold $X\subset Q$ representing the class $x$. Then $3\sigma(X)=p_1(X)=xPDp_1(Q)-x^3=3\sigma_x(Q)$ by \cite{Hirzebruch1966}, end of 9.2 or else by \cite{Skopenkov2008}, Submanifold Lemma.) | ||
| − | + | {{beginthm|Definition}} The '''Kreck invariant''' of two embeddings $f$ and $f'$ such that $W(f)=W(f')$ is defined by | |
$$\eta(f,f'):\equiv\frac{\sigma_{2A}(M_\varphi)}{16}= | $$\eta(f,f'):\equiv\frac{\sigma_{2A}(M_\varphi)}{16}= | ||
\frac{APDp_1(M_\varphi)-4A^3}{24}\mod d(W(f)),$$ | \frac{APDp_1(M_\varphi)-4A^3}{24}\mod d(W(f)),$$ | ||
| − | where $\varphi:\partial C_f\to\partial C_{f'}$ is a spin isomorphism and $A\in H_4(M)$ is a joint homology Seifert surface for $f$ and $f'$. Cf. \cite{Ekholm2001}, 4.1, \cite{Zhubr}. We have $2A\mod2=0=PDw_2(M_\varphi)$, so any closed connected oriented 4-submanifold of $M_\varphi$ representing the class $2A$ is spin, hence by the Rokhlin Theorem $\sigma_{2A}(M_\varphi)$ is indeed divisible by 16. The Kreck invariant is well-defined by \cite{Skopenkov2008}, Independence Lemma. | + | where $\varphi:\partial C_f\to\partial C_{f'}$ is a spin isomorphism and $A\in H_4(M)$ is a joint homology Seifert surface for $f$ and $f'$. Cf. \cite{Ekholm2001}, 4.1, \cite{Zhubr}. |
| + | {{endthm}} | ||
| + | |||
| + | We have $2A\mod2=0=PDw_2(M_\varphi)$, so any closed connected oriented 4-submanifold of $M_\varphi$ representing the class $2A$ is spin, hence by the Rokhlin Theorem $\sigma_{2A}(M_\varphi)$ is indeed divisible by 16. The Kreck invariant is well-defined by \cite{Skopenkov2008}, Independence Lemma. | ||
For $a\in H_1(N)$ fix an embedding $f':N\to\Rr^6$ such that $W(f')=a$ and define $\eta_a(f):=\eta(f,f')$. (We write $\eta_a(f)$ not $\eta_{f'}(f)$ for simplicity.) | For $a\in H_1(N)$ fix an embedding $f':N\to\Rr^6$ such that $W(f')=a$ and define $\eta_a(f):=\eta(f,f')$. (We write $\eta_a(f)$ not $\eta_{f'}(f)$ for simplicity.) | ||
| Line 76: | Line 76: | ||
{{endthm}} | {{endthm}} | ||
</wikitex> | </wikitex> | ||
| − | |||
| − | |||
| − | |||
| − | [[ | + | == Classification == |
| − | + | <wikitex>; | |
| − | { | + | <!--For notation and conventions see [[High_codimension_embeddings|high codimension embeddings]].--> |
| + | The results of this page are proved in \cite{Skopenkov2008} unless other references are given. | ||
| + | Let $N$ be a closed connected orientable 3-manifold. | ||
| + | {{beginthm|Classification Theorem}}\label{th7} The Whitney invariant | ||
| + | $$W:E^6_D(N)\to H_1(N)$$ | ||
| + | is surjective. For each $a\in H_1(N)$ the Kreck invariant | ||
| + | $$\eta_a:W^{-1}(u)\to\Zz_{d(a)}$$ | ||
| + | is bijective, where $d(a)$ is the divisibility of the projection of $a$ to the free part of $H_1(N)$. | ||
| + | {{endthm}} | ||
| + | |||
| + | Recall that for an abelian group $G$ the divisibility of zero is zero and the divisibility of $x\in G-\{0\}$ is $\max\{d\in\Zz\ | \ \text{there is }x_1\in G:\ x=dx_1\}$. [[Definition_of_the_Kreck_invariant_for_3-manifolds_in_the_6-space|Definition of the Kreck invariant]]. All isotopy classes of embeddings $N\to\Rr^6$ can be constructed (from a certain given embedding) using connected sum with embeddings $S^3\to\Rr^6$, see the construction in [[Classification_just_below_the _stable_range|classification just below the stable range]] and in [[Some_general_remarks|some general remarks]]. | ||
| + | |||
| + | {{beginthm|Corollary}}\label{co8} | ||
| + | *The Kreck invariant $\eta_0:E^6(N)\to\Zz$ is a 1--1 correspondence if $N$ is $S^3$ or an integral homology sphere \cite{Haefliger1966}, \cite{Hausmann1972}, \cite{Takase2006}. (For $N=S^3$ the Kreck invariant is also a group isomorphism; this does not follows from the Classification Theorem \ref{th7} but is proved in \cite{Haefliger1966}.) | ||
| + | *If $H_2(N)=0$ (i.e. $N$ is a rational homology sphere, e.g. $N=\Rr P^3$), then $E^6(N)$ is in (non-canonical) 1--1 correspondence with $\Zz\times H_1(N)$. | ||
| + | *Embeddings $S^1\times S^2\to\Rr^6$ with zero Whitney invariant are in 1--1 correspondence with $\Zz$, and for each integer $k\ne0$ there are exactly $k$ distinct (i.e. non-isotopic) embeddings $S^1\times S^2\to\Rr^6$ with the Whitney invariant $k$, cf. Corollary \ref{co10} below. | ||
| + | *The Whitney invariant $W:E^6(N_1\# N_2)\to H_1(N_1\# N_2)\cong H_1(N_1)\oplus H_1(N_2)$ is surjective and $\# W^{-1}(a_1\oplus a_2)=\#\Zz_{GCD(d(a_1),d(a_2))}$. | ||
| + | {{endthm}} | ||
| + | |||
| + | {{beginthm|Addendum}}\label{ad9} If $f:N\to\Rr^6$ is an embedding, $t$ is the generator of $E^6(S^3)\cong\Zz$ and $kt$ is a connected sum of $k$ copies of $t$, then | ||
| + | $$W(f\#kt)=W(f)\quad and\quad \eta_{W(f)}(f\#kt)\equiv\eta_{W(f)}(f)+k\mod d(W(f)).$$ | ||
| + | {{endthm}} | ||
| + | |||
| + | E. g. for $N=\Rr P^3$ the `connected sum' action of $E^6(S^3)$ on $E^6(N)$ is free while for $N=S^1\times S^2$ we have the following corollary. (We believe that this very concrete corollary or the case $N=\Rr P^3$ | ||
| + | are as non-trivial as the general case of the Classification Theorem.) | ||
| + | |||
| + | {{beginthm|Corollary}}\label{co10} | ||
| + | *There is an embedding $f=\Hud(3):S^1\times S^2\to\Rr^6$ such that for each knot $g:S^3\to\Rr^6$ the embedding $f\# g$ is isotopic to $f$. | ||
| + | *For each embedding $f:N\to\Rr^6$ such that $f(N)\subset\Rr^5$ (e.g. for the standard embedding $f:S^1\times S^2\to\Rr^6$) and each non-trivial knot $g:S^3\to\Rr^6$ the embedding $f\# g$ is not isotopic to $f$. | ||
| + | {{endthm}} | ||
| + | </wikitex> | ||
== References == | == References == | ||
Revision as of 09:32, 19 February 2010
| This page has been accepted for publication in the Bulletin of the Manifold Atlas. |
For notation and conventions throughout this page see high codimension embeddings.
Contents |
1 Examples
1.1 The Haefliger trefoil knot
Let us construct a smooth embedding 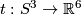 (which is a generator of
(which is a generator of 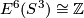 ) [Haefliger1962], 4.1. A miraculous property of this embedding is that it is not
) [Haefliger1962], 4.1. A miraculous property of this embedding is that it is not 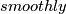 isotopic to the standard embedding, but is
isotopic to the standard embedding, but is 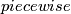
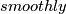 isotopic to the standard embedding.
isotopic to the standard embedding.
Denote coordinates in 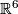 by
by 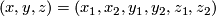 . The higher-dimensional trefoil knot
. The higher-dimensional trefoil knot 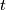 is obtained by joining
with two tubes the higher-dimensional
is obtained by joining
with two tubes the higher-dimensional 
 , i.e. the three spheres given by the following three systems of equations:
, i.e. the three spheres given by the following three systems of equations:
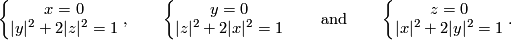
See Figures 3.5 and 3.6 of [Skopenkov2006].
1.2 The Hopf construction of an embedding 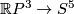
Represent 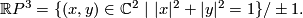 Define
Define
![\displaystyle Ho:\Rr P^3\to S^5\subset\Cc^3\quad\text{by}\quad Ho[(x,y)]=(x^2,2xy,y^2).](/images/math/d/7/a/d7a26b0af78cfc97ff3048bf1296424e.png)
It is easy to check that 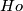 is an embedding. (The image of this embedding is given by the equations
is an embedding. (The image of this embedding is given by the equations 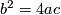 ,
, 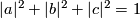 .)
.)
It would be interesting to obtain an explicit construction of an embedding 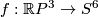 which is not isotopic to the composition of the Hopf embedding with the standard inclusion
which is not isotopic to the composition of the Hopf embedding with the standard inclusion 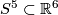 . (Such an embedding
. (Such an embedding  is unique up to PL isotopy by classification just below the stable range.)
is unique up to PL isotopy by classification just below the stable range.)
1.3 Algebraic embeddings from the theory of integrable systems
Some 3-manifolds appear in the theory of integrable systems together with their embeddings into 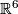 (given by a system of algebraic equations) [Bolsinov&Fomenko2004], Chapter 14. E.g. the following system of equations corresponds to the Euler integrability case:
(given by a system of algebraic equations) [Bolsinov&Fomenko2004], Chapter 14. E.g. the following system of equations corresponds to the Euler integrability case:
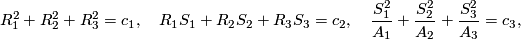
where 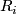 and
and 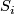 are variables while
are variables while 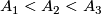 and
and 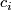 are constants.
This defines embeddings of
are constants.
This defines embeddings of  ,
, 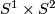 or
or 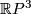 into
into 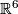 .
.
2 Invariants
Let  be a closed connected orientable 3-manifold. An orientation-preserving diffeomorphism
be a closed connected orientable 3-manifold. An orientation-preserving diffeomorphism 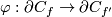 such that
such that 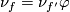 is simply called an
is simply called an 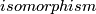 . For an isomorphism
. For an isomorphism 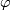 denote
denote
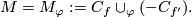
An isomorphism 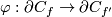 is called
is called 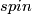 , if
, if 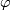 over
over  is defined by an isotopy between the restrictions of
is defined by an isotopy between the restrictions of  and
and  to
to  . A spin isomorphism exists because the restrictions to
. A spin isomorphism exists because the restrictions to  of
of  and
and  are isotopic (see the definition of the Whitney invariant in classification just below the stable range) and because
are isotopic (see the definition of the Whitney invariant in classification just below the stable range) and because 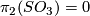 . If
. If 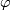 is a spin isomorphism, then
is a spin isomorphism, then 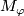 is spin [Skopenkov2008], Spin Lemma.
is spin [Skopenkov2008], Spin Lemma.
Denote by 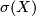 the signature of a 4-manifold
the signature of a 4-manifold  . Denote by
. Denote by 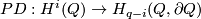 and
and 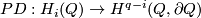 Poincar\'e duality (in any manifold
Poincar\'e duality (in any manifold 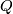 ). For
). For 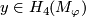 and a
and a  -submanifold
-submanifold 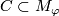 (e.g.
(e.g. 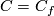 or
or 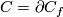 ) denote
) denote
![\displaystyle y\cap C:=PD[(PDy)|_C]\in H_{k-2}(C,\partial C).](/images/math/7/a/7/7a7ca8e79ee8514370b1eb63fd16a913.png)
If  is represented by a closed oriented 4-submanifold
is represented by a closed oriented 4-submanifold 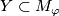 in general position to
in general position to  , then
, then 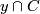 is represented by
is represented by  .
.
A 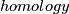
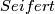
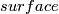 for
for  is the image
is the image 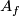 of the fundamental class
of the fundamental class ![[N]](/images/math/3/5/8/3581986b0e7b591acd8d60e6ee096f5d.png) under the composition
under the composition 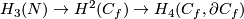 of the Alexander and Poincar\'e duality isomorphisms. A
of the Alexander and Poincar\'e duality isomorphisms. A 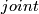
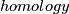
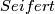
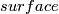 for
for  and
and  is a class
is a class 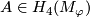 such that
such that
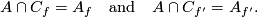
If 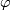 is a spin isomorphism and
is a spin isomorphism and 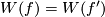 , then there is a joint homology Seifert surface for
, then there is a joint homology Seifert surface for  and
and  [Skopenkov2008], Agreement Lemma.
[Skopenkov2008], Agreement Lemma.
We identify with  the zero-dimensional homology groups and the
the zero-dimensional homology groups and the  -dimensional cohomology groups of closed connected oriented
-dimensional cohomology groups of closed connected oriented  -manifolds. The intersection products in 6-manifolds are omitted from the notation. For a closed connected oriented 6-manifold
-manifolds. The intersection products in 6-manifolds are omitted from the notation. For a closed connected oriented 6-manifold 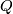 and
and 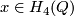 denote by
denote by
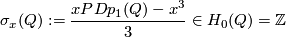
the virtual signature of 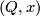 .
(Since
.
(Since ![H_4(Q)\cong[Q,\Cc P^\infty]](/images/math/6/0/a/60aee1380b3beee7cca076a781f916ed.png) , there is a closed connected oriented 4-submanifold
, there is a closed connected oriented 4-submanifold 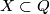 representing the class
representing the class  . Then
. Then 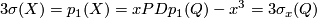 by [Hirzebruch1966], end of 9.2 or else by [Skopenkov2008], Submanifold Lemma.)
by [Hirzebruch1966], end of 9.2 or else by [Skopenkov2008], Submanifold Lemma.)
Definition 2.1. The Kreck invariant of two embeddings  and
and  such that
such that 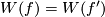 is defined by
is defined by
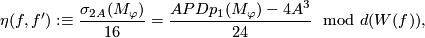
where 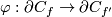 is a spin isomorphism and
is a spin isomorphism and 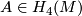 is a joint homology Seifert surface for
is a joint homology Seifert surface for  and
and  . Cf. [Ekholm2001], 4.1, [Zhubr].
. Cf. [Ekholm2001], 4.1, [Zhubr].
We have 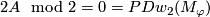 , so any closed connected oriented 4-submanifold of
, so any closed connected oriented 4-submanifold of 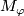 representing the class
representing the class 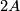 is spin, hence by the Rokhlin Theorem
is spin, hence by the Rokhlin Theorem 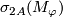 is indeed divisible by 16. The Kreck invariant is well-defined by [Skopenkov2008], Independence Lemma.
is indeed divisible by 16. The Kreck invariant is well-defined by [Skopenkov2008], Independence Lemma.
For 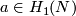 fix an embedding
fix an embedding 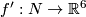 such that
such that 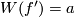 and define
and define 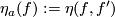 . (We write
. (We write 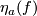 not
not 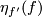 for simplicity.)
for simplicity.)
The choice of the other orientation for  (resp.
(resp. 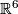 ) will in general give rise to different values for the Kreck invariant. But such a choice only permutes the bijection
) will in general give rise to different values for the Kreck invariant. But such a choice only permutes the bijection 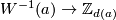 (resp. replaces it with the bijection
(resp. replaces it with the bijection 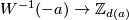 ).
).
Let us present a formula for the Kreck invariant analogous to [Guillou&Marin1986], Remarks to the four articles of Rokhlin, II.2.7 and III.excercises.IV.3, [Takase2004], Corollary 6.5, [Takase2006], Proposition 4.1. This formula is useful when an embedding goes through 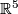 or is given by a system of equations (because we can obtain a `Seifert surface' by changing the equality to the inequality in one
of the equations). See also
[Moriyama, Integral formula for an extension of Haeliger's embedding invariant].
or is given by a system of equations (because we can obtain a `Seifert surface' by changing the equality to the inequality in one
of the equations). See also
[Moriyama, Integral formula for an extension of Haeliger's embedding invariant].
The Kreck Invariant Lemma 2.2.[Skopenkov2008]
Let 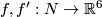 be two embeddings such that
be two embeddings such that 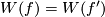 ,
, 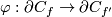 a spin isomorphism,
a spin isomorphism, 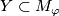 a closed connected oriented 4-submanifold representing a joint homology Seifert surface and
a closed connected oriented 4-submanifold representing a joint homology Seifert surface and 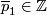 ,
, 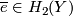 are the Pontryagin number and Poincar\'e dual of the Euler classes of the normal bundle of
are the Pontryagin number and Poincar\'e dual of the Euler classes of the normal bundle of  in
in 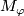 . Then
. Then
![\displaystyle \frac{\sigma_{2[Y]}(M_\varphi)}{16}=\frac{\sigma(Y)-\overline p_1}8= \frac{\sigma(Y)-\overline e\cap\overline e}8.](/images/math/9/7/6/976d016617f48101c3311526cf28aa4a.png)
3 Classification
The results of this page are proved in [Skopenkov2008] unless other references are given.
Let  be a closed connected orientable 3-manifold.
be a closed connected orientable 3-manifold.
Classification Theorem 3.1. The Whitney invariant
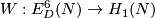
is surjective. For each 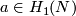 the Kreck invariant
the Kreck invariant
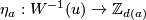
is bijective, where 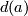 is the divisibility of the projection of
is the divisibility of the projection of  to the free part of
to the free part of 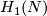 .
.
Recall that for an abelian group  the divisibility of zero is zero and the divisibility of
the divisibility of zero is zero and the divisibility of 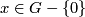 is
is 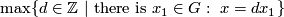 . Definition of the Kreck invariant. All isotopy classes of embeddings
. Definition of the Kreck invariant. All isotopy classes of embeddings 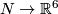 can be constructed (from a certain given embedding) using connected sum with embeddings
can be constructed (from a certain given embedding) using connected sum with embeddings 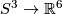 , see the construction in classification just below the stable range and in some general remarks.
, see the construction in classification just below the stable range and in some general remarks.
Corollary 3.2.
- The Kreck invariant
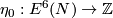 is a 1--1 correspondence if
is a 1--1 correspondence if  is
is  or an integral homology sphere [Haefliger1966], [Hausmann1972], [Takase2006]. (For
or an integral homology sphere [Haefliger1966], [Hausmann1972], [Takase2006]. (For 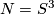 the Kreck invariant is also a group isomorphism; this does not follows from the Classification Theorem 3.1 but is proved in [Haefliger1966].)
the Kreck invariant is also a group isomorphism; this does not follows from the Classification Theorem 3.1 but is proved in [Haefliger1966].)
- If
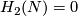 (i.e.
(i.e.  is a rational homology sphere, e.g.
is a rational homology sphere, e.g. 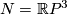 ), then
), then 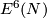 is in (non-canonical) 1--1 correspondence with
is in (non-canonical) 1--1 correspondence with 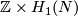 .
.
- Embeddings
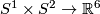 with zero Whitney invariant are in 1--1 correspondence with
with zero Whitney invariant are in 1--1 correspondence with  , and for each integer
, and for each integer 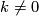 there are exactly
there are exactly  distinct (i.e. non-isotopic) embeddings
distinct (i.e. non-isotopic) embeddings  with the Whitney invariant
with the Whitney invariant  , cf. Corollary 3.4 below.
, cf. Corollary 3.4 below.
- The Whitney invariant
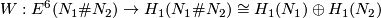 is surjective and
is surjective and 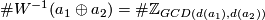 .
.
Addendum 3.3. If 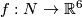 is an embedding,
is an embedding, 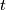 is the generator of
is the generator of 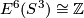 and
and 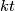 is a connected sum of
is a connected sum of  copies of
copies of 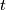 , then
, then
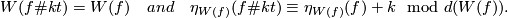
E. g. for 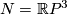 the `connected sum' action of
the `connected sum' action of  on
on 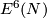 is free while for
is free while for 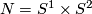 we have the following corollary. (We believe that this very concrete corollary or the case
we have the following corollary. (We believe that this very concrete corollary or the case 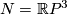 are as non-trivial as the general case of the Classification Theorem.)
are as non-trivial as the general case of the Classification Theorem.)
Corollary 3.4.
- There is an embedding
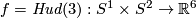 such that for each knot
such that for each knot 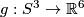 the embedding
the embedding 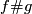 is isotopic to
is isotopic to  .
.
- For each embedding
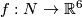 such that
such that 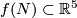 (e.g. for the standard embedding
(e.g. for the standard embedding 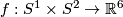 ) and each non-trivial knot
) and each non-trivial knot 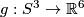 the embedding
the embedding 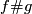 is not isotopic to
is not isotopic to  .
.
4 References
- [Bolsinov&Fomenko2004] A. V. Bolsinov and A. T. Fomenko, Integrable Hamiltonian systems, Chapman \& Hall/CRC, Boca Raton, FL, 2004. MR2036760 (2004j:37106) Zbl 1056.37075
- [Ekholm2001] T. Ekholm, Differential 3-knots in 5-space with and without self-intersections, Topology 40 (2001), no.1, 157–196. MR1791271 (2001h:57033) Zbl 0964.57029
- [Guillou&Marin1986] L. Guillou and A.Marin, Eds., A la r\'echerche de la topologie perdue, 1986, Progress in Math., 62, Birkhauser, Basel
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 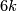 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Hausmann1972] J. Hausmann, Plongements de sphères d'homologie, C. R. Acad. Sci. Paris Sér. A-B 275 (1972), A963–965. MR0315727 (47 #4276) Zbl 0244.57005
- [Hirzebruch1966] F. Hirzebruch, Topological methods in algebraic geometry, Springer-Verlag, New York, 1966. MR0202713 (34 #2573) Zbl 0843.14009
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2008] A. Skopenkov, A classification of smooth embeddings of 3-manifolds in 6-space, Math. Z. 260 (2008), no.3, 647–672. Available at the arXiv:0603429MR2434474 (2010e:57028) Zbl 1167.57013
- [Takase2004] M. Takase, A geometric formula for Haefliger knots, Topology 43 (2004), no.6, 1425–1447. MR2081431 (2005e:57032) Zbl 1060.57021
- [Takase2006] M. Takase, Homology 3-spheres in codimension three, Internat. J. Math. 17 (2006), no.8, 869–885.
arxiv:math/0506464 MR2261638 (2007g:57049) Zbl 1113.57013
|
This page has not been refereed. The information given here might be incomplete or provisional. |