1-manifolds
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 08:32, 18 July 2013 and the changes since publication. |
Contents |
1 Introduction
According to general definition of manifold, a manifold of dimension 1 is a topological space which is second countable (i.e., has a countable base), satisfies the Hausdorff axiom (any two different point in it have disjoint neighborhoods) and each point of which has a neighborhood homeomorphic either to line  or half-line
or half-line 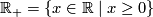 .
.
Manifolds of dimension 1 are called curves, but this name may lead to a confusion, because many mathematical objects share it. Even in the context of topology, the term curve may mean not only a manifold of dimension 1 with an additional structure, but, for instance, an immersion
of a smooth manifold of dimension 1 to Euclidean space 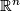 . To be on the safe side, we use an
unambiguous term manifold of dimension 1 or 1-manifold.
. To be on the safe side, we use an
unambiguous term manifold of dimension 1 or 1-manifold.
2 Construction and examples
Real line 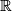 , half-line
, half-line 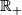 , circle
, circle 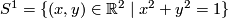 , closed interval
, closed interval
![I=[0,1]](/images/math/1/c/a/1ca01533a825141b051c7492a6fa6427.png) .
.
3 Invariants
Let  be a 1-manifold: let
be a 1-manifold: let 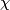 denote the Euler characteristic,
denote the Euler characteristic, 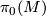 the number of connected components of
the number of connected components of  and
and 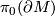 the connected components of the boundary of
the connected components of the boundary of  .
.
-
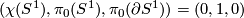 ,
,
-
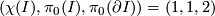 ,
,
-
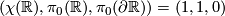 ,
,
-
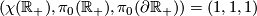 ,
,
4 Classification and characterization
Any 1-manifold is homeomorphic to disjoint sum of its connected components. The connected components of a 1-manifold are 1-manifolds.
Two manifolds are homeomorphic iff there exists a one-to-one correspondence between their components such that the corresponding components are homeomorphic.
Any connected 1-manifold is homeomorphic either to real line 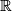 , half-line
, half-line 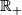 , circle
, circle 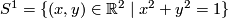 , closed interval
, closed interval ![I=[0,1]](/images/math/1/c/a/1ca01533a825141b051c7492a6fa6427.png) .
.
Any connected closed 1-manifold is homeomorphic to the circle  .
.
Any connected compact 1-manifold with non-empty boundary is homeomorphic to the interval  .
.
Any connected non-compact 1-manifold without boundary is homeomorphic to the line 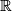 .
.
Any connected non-compact 1-manifold with non-empty boundary is homeomorphic to the half-line 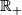 .
.
Thus we see that for connected 1-manifolds two invariants, compactness and presence of boundary, taking each two values form a complete system of topological invariants.
The classification theorems stated above can be deduced from the following simple Lemma: a Hausdorff topological space which can be covered by two open subsets which are homeomorphic to 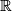 is homeomorphic either to
is homeomorphic either to
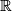 or
or  .
.
5 Further discussion
The results above solve topological classification problem for 1-manifolds in the most effective way that one can wish. Surprisingly, many textbooks manage not to mention it.
6 References
|
This page has not been refereed. The information given here might be incomplete or provisional. |