1-manifolds
| Line 16: | Line 16: | ||
Manifolds of dimension 1 are called ''curves'', but this name may lead to a confusion, because many mathematical objects share it. Even in the context of topology, the term ''curve'' may mean not only a manifold of dimension 1 with an additional structure, but, for instance, an immersion | Manifolds of dimension 1 are called ''curves'', but this name may lead to a confusion, because many mathematical objects share it. Even in the context of topology, the term ''curve'' may mean not only a manifold of dimension 1 with an additional structure, but, for instance, an immersion | ||
| − | of a smooth manifold of dimension 1 to Euclidean space $\ | + | of a smooth manifold of dimension 1 to Euclidean space $\Rr^n$. To be on the safe side, we use an |
unambiguous term ''manifold of dimension 1'' or ''1-manifold''. | unambiguous term ''manifold of dimension 1'' or ''1-manifold''. | ||
</wikitex> | </wikitex> | ||
| Line 30: | Line 30: | ||
* Closed interval $I=[0,1]$ | * Closed interval $I=[0,1]$ | ||
</wikitex> | </wikitex> | ||
| − | |||
| − | |||
<!-- COMMENT O.V.: | <!-- COMMENT O.V.: | ||
About usage of Euler characteristic. | About usage of Euler characteristic. | ||
| Line 55: | Line 53: | ||
==== Reduction to classification of connected manifolds ==== | ==== Reduction to classification of connected manifolds ==== | ||
| + | <!-- COMMMENT O.V. | ||
| + | This subsection has to be moved to some general theory of manifolds, because it contains almost nothing specific about dimension 1 (at the only occasion 1-manifolds have to be replaced by $n$-manifolds). | ||
| + | Only a reference or, rather, a link to this must be left here. | ||
| + | END OF COMMENT--> | ||
| + | |||
<wikitex>; | <wikitex>; | ||
| − | Any manifold is homeomorphic to disjoint sum of its connected components. | + | Any manifold is homeomorphic to the disjoint sum of its connected components. |
| + | <!-- Should we have here a reference to a definition of disjoint sum of topological spaces? --> | ||
| − | A connected component of a 1-manifold is a 1- | + | A connected component of a 1-manifold is a 1-manifold. |
Two manifolds are homeomorphic iff there exists a one-to-one correspondence between their components | Two manifolds are homeomorphic iff there exists a one-to-one correspondence between their components | ||
| Line 93: | Line 97: | ||
The theorems above solve the topological classification problem for 1-manifolds in the most effective way that one can wish. Surprisingly, many Topology textbooks manage not to mention this fundamental result. | The theorems above solve the topological classification problem for 1-manifolds in the most effective way that one can wish. Surprisingly, many Topology textbooks manage not to mention this fundamental result. | ||
| + | |||
| + | If we enlarge the collection of spaces by getting rid of the Hausdorff property, then the number of topological types of connected spaces becomes uncountable. Indeed, one can take two copies of line $\Rr$ and identify | ||
| + | an open set in one of them with its copy in the other one by the identity map. The result satisfies all the | ||
| + | requirements from the definition of 1-manifold except the Hausdorff axiom. | ||
</wikitex> | </wikitex> | ||
=== Corollaries === | === Corollaries === | ||
| Line 108: | Line 116: | ||
''Any 1-manifold admits a smooth structure.'' | ''Any 1-manifold admits a smooth structure.'' | ||
| − | If smooth 1-manifolds $X$ and $Y$ are homeomorphic, then they are also diffeomorphic. | + | If smooth 1-manifolds $X$ and $Y$ are homeomorphic, then they are also diffeomorphic. Moreover, <br> |
| − | Moreover, any homeomorphism $X\to Y$ can be approximated in the $C^0$-topology by a diffeomorphism. | + | ''any homeomorphism $X\to Y$ can be approximated in the $C^0$-topology by a diffeomorphism.'' |
| − | Technically this can be considered as a corollary of the following simple theorem: | + | Technically this can be considered as a corollary of the following simple theorem:<br> |
| − | a map $\Rr\to\Rr$ is a homeomorphism iff it is a continuous monotone bijection. | + | ''a map $\Rr\to\Rr$ is a homeomorphism iff it is a continuous monotone bijection.'' |
</wikitex> | </wikitex> | ||
== Invariants == | == Invariants == | ||
<wikitex>; | <wikitex>; | ||
| − | As follows from the classification theorems, '' | + | As follows from the classification theorems, |
| − | play fundamental role in topology of 1-manifolds. Homotopy invariants are extremely simple. | + | * the ''number of connected components'', |
| + | * ''compactness of a connected component'', | ||
| + | * and ''boundary'' of a connected component<br> | ||
| + | play fundamental role in topology of 1-manifolds. | ||
| + | |||
| + | Homotopy invariants are extremely simple. | ||
</wikitex> | </wikitex> | ||
| Line 124: | Line 137: | ||
==== Connected sums ==== | ==== Connected sums ==== | ||
<wikitex>; | <wikitex>; | ||
| + | The notion of connected sum is defined for 1-manifolds, but it does not work in the same way as for manifolds of higher dimensions. | ||
| + | |||
| + | Recall that a manifold $X$ of dimension $n$ is a ''connected sum'' of manifolds $A$ and $B$ | ||
| + | if there are $n$-disks $D_A\subset A$ and $D_B\subset B$ and a homeomorphism $h:D_A\to D_B$ such that $X$ is homeomorphic to $(A\cup_h B)\smallsetminus\operatorname{Int}D_A$ (that is to the result of attaching of $A$ | ||
| + | to $B$ by $h$ with the image of interior of the identified disks $D_A$ and $D_B$ removed). One writes $X=A\sharp B$, however the topology of $X$ may depend not only on $A$ and $B$, but also on $D_A$, $D_B$ and $h$. The dependence disappears if | ||
| + | all connected components of $A$ are homeomorphic to each other, all connected components of $B$ are homeomorphic to each other, and a homeomorphism | ||
| + | $D_A\to D_A$ reversing orientation can be extended to a homeomorphism $A\to A$, or a homeomorphism | ||
| + | $D_B\to D_B$ reversing orientation can be extended to a homeomorphism $B\to B$. For a collection of manifolds satisfying these conditions, a connected sum can be considered as operation on topological types. | ||
| + | |||
| + | <!-- COMMENT BY O.V. The paragraph above should be moved to a general theory of manifolds, but a reference to it | ||
| + | must be left END OF COMMENT --> | ||
| + | |||
The very term ''connected sum'' is compromised in dimension 1. Indeed, a connected sum | The very term ''connected sum'' is compromised in dimension 1. Indeed, a connected sum | ||
of connected 1-manifolds may be not connected. For example a connected sum of two | of connected 1-manifolds may be not connected. For example a connected sum of two | ||
| Line 129: | Line 154: | ||
Moreover, connected sum, as an operation on topological types of 1-manifolds, is not well-defined. | Moreover, connected sum, as an operation on topological types of 1-manifolds, is not well-defined. | ||
| − | Indeed, both $I\amalg\Rr$ and $\Rr_+\amalg\Rr_+$ can be presented as a connected sum of | + | Indeed, both disjoint sums $I\amalg\Rr$ and $\Rr_+\amalg\Rr_+$ can be presented as a connected sum of |
two copies of $\Rr_+$. | two copies of $\Rr_+$. | ||
| Line 135: | Line 160: | ||
==== Orientations ==== | ==== Orientations ==== | ||
<wikitex>; | <wikitex>; | ||
| − | Orientation of a 1-manifold can be interpreted | + | Orientation of a 1-manifold can be interpreted via linear or cyclic orderings of their points. |
| − | An orientation of a | + | An orientation of a connected non-closed 1-manifold is a |
linear order on the set of its points such that the corresponding | linear order on the set of its points such that the corresponding | ||
interval topology coincides with the topology of this manifold. | interval topology coincides with the topology of this manifold. | ||
| Line 149: | Line 174: | ||
Any 1-manifold admits an orientation. | Any 1-manifold admits an orientation. | ||
| − | Half-line $\Rr_+$ does not admit a homeomorphism reversing orientation. Any connected 1-manifold non-homeomorphic to $\Rr_+$ admits an orientation reversing map. | + | Half-line $\Rr_+$ does not admit a homeomorphism reversing orientation. Any connected 1-manifold non-homeomorphic to $\Rr_+$ admits an orientation reversing map. Thus, there are 5 topological types of oriented connected 1-manifolds. |
</wikitex> | </wikitex> | ||
==== Mapping class groups ==== | ==== Mapping class groups ==== | ||
<wikitex>; | <wikitex>; | ||
| + | Recall that the ''mapping class group'' of a manifold $X$ is the quotient group of the group $\operatorname{Homeo} (X)$ of all homeomorphisms $X\to X$ by the normal subgroup of homeomorphisms isotopic to the identity. | ||
| + | In other words, the mapping class group of $X$ is $\pi_0(\operatorname{Homeo}(X))$. | ||
| + | A reversing orientation homeomorphism cannot be isotopic to the identity. For an auto-homeomorphism of a | ||
| + | connected 1-manifold this is the only obstruction to being isotopic to the identity. Therefore $\pi_0(\operatorname{Homeo}(S^1))=\pi_0(\operatorname{Homeo}(\Rr))=\pi_0(\operatorname{Homeo}(I))=\mathbb{Z}/_2$, | ||
| + | while $\pi_0(\operatorname{Homeo} \Rr_+)=0$. | ||
</wikitex> | </wikitex> | ||
==== Finite group actions ==== | ==== Finite group actions ==== | ||
Revision as of 18:06, 1 October 2009
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 08:32, 18 July 2013 and the changes since publication. |
Contents |
1 Introduction
According to the general definition of manifold, a manifold of dimension 1 is a topological space which is second countable (i.e., its topological structure has a countable base), satisfies the Hausdorff axiom (any two different points have disjoint neighborhoods) and each point of which has a neighborhood homeomorphic either to line  or half-line
or half-line 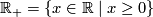 .
.
Manifolds of dimension 1 are called curves, but this name may lead to a confusion, because many mathematical objects share it. Even in the context of topology, the term curve may mean not only a manifold of dimension 1 with an additional structure, but, for instance, an immersion
of a smooth manifold of dimension 1 to Euclidean space  . To be on the safe side, we use an
unambiguous term manifold of dimension 1 or 1-manifold.
. To be on the safe side, we use an
unambiguous term manifold of dimension 1 or 1-manifold.
2 Examples
- Real line
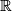
- Half-line
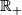
- Circle
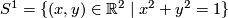
- Closed interval
![I=[0,1]](/images/math/1/c/a/1ca01533a825141b051c7492a6fa6427.png)
3 Classification
3.1 Reduction to classification of connected manifolds
Any manifold is homeomorphic to the disjoint sum of its connected components.
A connected component of a 1-manifold is a 1-manifold.
Two manifolds are homeomorphic iff there exists a one-to-one correspondence between their components such that the corresponding components are homeomorphic.
3.2 Topological classification of connected 1-manifolds
Theorem 3.1. Any connected 1-manifold is homeomorphic to one of the following 4 manifolds:
- real line
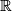
- half-line
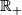
- circle
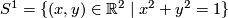
- closed interval
![I=[0,1]](/images/math/1/c/a/1ca01533a825141b051c7492a6fa6427.png) .
.
No two of these manifolds are homeomorphic to each other.
3.3 Characterizing the topological type of a connected 1-manifold
- Any connected closed 1-manifold is homeomorphic to
 .
.
- Any connected compact 1-manifold with non-empty boundary is homeomorphic to
 .
.
- Any connected non-compact 1-manifold without boundary is homeomorphic to
 .
.
- Any connected non-compact 1-manifold with non-empty boundary is homeomorphic to
 .
.
Thus for connected 1-manifolds two invariants, compactness and presence of boundary form a complete system of topological invariants. Each of the invariants takes two values.
3.4 Remarks
Proofs of the results above are elementary. The core of them is the following simple
 is homeomorphic either to
is homeomorphic either to  or
or  .
.The theorems above solve the topological classification problem for 1-manifolds in the most effective way that one can wish. Surprisingly, many Topology textbooks manage not to mention this fundamental result.
If we enlarge the collection of spaces by getting rid of the Hausdorff property, then the number of topological types of connected spaces becomes uncountable. Indeed, one can take two copies of line  and identify
an open set in one of them with its copy in the other one by the identity map. The result satisfies all the
requirements from the definition of 1-manifold except the Hausdorff axiom.
and identify
an open set in one of them with its copy in the other one by the identity map. The result satisfies all the
requirements from the definition of 1-manifold except the Hausdorff axiom.
3.5 Corollaries
3.5.1 Homotopy classification of 1-manifolds
Each connected 1-manifold is either contractible, or homotopy equivalent to circle.
3.5.2 0-manifolds cobordant to zero
A compact 0-manifold  bounds a compact 1-manifold iff the number of points in
bounds a compact 1-manifold iff the number of points in  is even.
is even.
3.5.3 Smooth structures
Any 1-manifold admits a smooth structure.
If smooth 1-manifolds  and
and  are homeomorphic, then they are also diffeomorphic. Moreover,
are homeomorphic, then they are also diffeomorphic. Moreover,
any homeomorphism 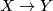 can be approximated in the
can be approximated in the 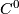 -topology by a diffeomorphism.
-topology by a diffeomorphism.
Technically this can be considered as a corollary of the following simple theorem:
a map 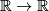 is a homeomorphism iff it is a continuous monotone bijection.
is a homeomorphism iff it is a continuous monotone bijection.
4 Invariants
As follows from the classification theorems,
- the number of connected components,
- compactness of a connected component,
- and boundary of a connected component
play fundamental role in topology of 1-manifolds.
Homotopy invariants are extremely simple.
5 Further discussion
5.1 Connected sums
The notion of connected sum is defined for 1-manifolds, but it does not work in the same way as for manifolds of higher dimensions.
Recall that a manifold  of dimension
of dimension  is a connected sum of manifolds
is a connected sum of manifolds  and
and  if there are
if there are  -disks
-disks 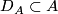 and
and 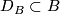 and a homeomorphism
and a homeomorphism 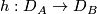 such that
such that  is homeomorphic to
is homeomorphic to 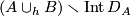 (that is to the result of attaching of
(that is to the result of attaching of  to
to  by
by  with the image of interior of the identified disks
with the image of interior of the identified disks 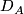 and
and 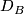 removed). One writes
removed). One writes 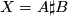 , however the topology of
, however the topology of  may depend not only on
may depend not only on  and
and  , but also on
, but also on 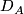 ,
, 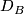 and
and  . The dependence disappears if
all connected components of
. The dependence disappears if
all connected components of  are homeomorphic to each other, all connected components of
are homeomorphic to each other, all connected components of  are homeomorphic to each other, and a homeomorphism
are homeomorphic to each other, and a homeomorphism
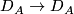 reversing orientation can be extended to a homeomorphism
reversing orientation can be extended to a homeomorphism 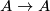 , or a homeomorphism
, or a homeomorphism
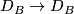 reversing orientation can be extended to a homeomorphism
reversing orientation can be extended to a homeomorphism 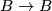 . For a collection of manifolds satisfying these conditions, a connected sum can be considered as operation on topological types.
. For a collection of manifolds satisfying these conditions, a connected sum can be considered as operation on topological types.
The very term connected sum is compromised in dimension 1. Indeed, a connected sum
of connected 1-manifolds may be not connected. For example a connected sum of two
copies of  is a disjoint sum of two copies of
is a disjoint sum of two copies of  .
.
Moreover, connected sum, as an operation on topological types of 1-manifolds, is not well-defined.
Indeed, both disjoint sums  and
and 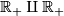 can be presented as a connected sum of
two copies of
can be presented as a connected sum of
two copies of  .
.
5.2 Orientations
Orientation of a 1-manifold can be interpreted via linear or cyclic orderings of their points.
An orientation of a connected non-closed 1-manifold is a linear order on the set of its points such that the corresponding interval topology coincides with the topology of this manifold.
An orientation of a connected closed 1-manifold is a cyclic order on the set of its points such that the topology of this cyclic order coincides with the topology of the 1-manifold.
An orientation of an arbitrary 1-manifold is a collection of orientations of its connected components (each component is equipped with an orientation).
Any 1-manifold admits an orientation.
Half-line  does not admit a homeomorphism reversing orientation. Any connected 1-manifold non-homeomorphic to
does not admit a homeomorphism reversing orientation. Any connected 1-manifold non-homeomorphic to  admits an orientation reversing map. Thus, there are 5 topological types of oriented connected 1-manifolds.
admits an orientation reversing map. Thus, there are 5 topological types of oriented connected 1-manifolds.
5.3 Mapping class groups
Recall that the mapping class group of a manifold  is the quotient group of the group
is the quotient group of the group 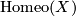 of all homeomorphisms
of all homeomorphisms 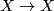 by the normal subgroup of homeomorphisms isotopic to the identity.
In other words, the mapping class group of
by the normal subgroup of homeomorphisms isotopic to the identity.
In other words, the mapping class group of  is
is  .
.
A reversing orientation homeomorphism cannot be isotopic to the identity. For an auto-homeomorphism of a
connected 1-manifold this is the only obstruction to being isotopic to the identity. Therefore 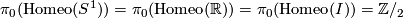 ,
while
,
while 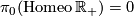 .
.
5.4 Finite group actions
5.5 Surgery
6 References
|
This page has not been refereed. The information given here might be incomplete or provisional. |