1-manifolds
| Line 13: | Line 13: | ||
== Introduction == | == Introduction == | ||
<wikitex>; | <wikitex>; | ||
| − | According to general definition of manifold, a manifold of dimension 1 is a topological space which is second countable (i.e., has a countable base), satisfies the Hausdorff axiom (any two different | + | According to the general definition of manifold, a manifold of dimension 1 is a topological space which is second countable (i.e., its topological structure has a countable base), satisfies the Hausdorff axiom (any two different points have disjoint neighborhoods) and each point of which has a neighborhood homeomorphic either to line $\Rr $ or half-line $\Rr_+=\{x\in\Rr\mid x\ge0\}$. |
Manifolds of dimension 1 are called ''curves'', but this name may lead to a confusion, because many mathematical objects share it. Even in the context of topology, the term ''curve'' may mean not only a manifold of dimension 1 with an additional structure, but, for instance, an immersion | Manifolds of dimension 1 are called ''curves'', but this name may lead to a confusion, because many mathematical objects share it. Even in the context of topology, the term ''curve'' may mean not only a manifold of dimension 1 with an additional structure, but, for instance, an immersion | ||
| Line 20: | Line 20: | ||
</wikitex> | </wikitex> | ||
| − | == | + | == Examples == |
<wikitex>; | <wikitex>; | ||
| − | Real line $\mathbb R$ | + | * Real line $\mathbb R$ |
| − | + | ||
| − | + | ||
| − | + | * Half-line $\mathbb R_+$ | |
| − | + | ||
| − | + | * Circle $S^1=\{(x,y)\in\Rr^2\mid x^2+y^2=1\}$ | |
| − | + | ||
| − | * $ | + | * Closed interval $I=[0,1]$ |
| − | + | ||
| − | * $ | + | |
| − | + | ||
</wikitex> | </wikitex> | ||
| − | == | + | |
| + | <!-- COMMENT O.V.: | ||
| + | About usage of Euler characteristic. | ||
| + | |||
| + | A non-compact space has many Euler characteristics. The notion of Euler characteristic depends | ||
| + | on the properties that one wants to preserve. If one wants to have invariance under homotopy equivalences, | ||
| + | then the additivity would be lost. If one wants to keep additivity, then it is not the alternating sum of Betti numbers. If one wants to keep topological invariance and additivity, then | ||
| + | $\chi(\Rr)=\chi(I)-2\chi(pt)=1-2=-1$, similarly $\chi(\Rr_+)=0$. In all the cases under consideration | ||
| + | the latter Euler characteristic is the alternating sum of the ranks of homology groups with closed support | ||
| + | (Borel-Moore homology). Pretty legitimate! | ||
| + | |||
| + | I would not recommend to use the Euler characteristic in a non-compact situation without a detailed | ||
| + | specification of the definition. | ||
| + | |||
| + | The problem of recognizing of the topological type is solved by the two invariants that I mentioned below: | ||
| + | compactness and presence of boundary. Other invariants can be used and deserve consideration. | ||
| + | However, I suggest to place the section Invariants after the section Classification. | ||
| + | |||
| + | END OF COMMENT | ||
| + | --> | ||
| + | |||
| + | == Classification == | ||
| + | |||
| + | ==== Reduction to classification of connected manifolds ==== | ||
<wikitex>; | <wikitex>; | ||
| − | Any | + | Any manifold is homeomorphic to disjoint sum of its connected components. |
| + | |||
| + | A connected component of a 1-manifold is a 1-manifolds. | ||
Two manifolds are homeomorphic iff there exists a one-to-one correspondence between their components | Two manifolds are homeomorphic iff there exists a one-to-one correspondence between their components | ||
such that the corresponding components are homeomorphic. | such that the corresponding components are homeomorphic. | ||
| + | </wikitex> | ||
| + | ==== Topological classification of connected 1-manifolds ==== | ||
| + | <wikitex>; | ||
| + | {{beginthm|Theorem}} Any connected 1-manifold is homeomorphic to one of the following 4 manifolds: | ||
| + | * real line $\mathbb R$ | ||
| + | * half-line $\mathbb R_+$ | ||
| + | * circle $S^1=\{(x,y)\in\Rr^2\mid x^2+y^2=1\}$ | ||
| + | * closed interval $I=[0,1]$. | ||
| + | No two of these manifolds are homeomorphic to each other. | ||
| + | {{endthm}} | ||
| + | </wikitex> | ||
| + | ==== Characterizing the topological type of a connected 1-manifold ==== | ||
| + | <wikitex>; | ||
| + | * Any connected closed 1-manifold is homeomorphic to $S^1$. | ||
| − | Any connected 1-manifold is homeomorphic | + | * Any connected compact 1-manifold with non-empty boundary is homeomorphic to $I$. |
| − | Any connected | + | * Any connected non-compact 1-manifold without boundary is homeomorphic to $\Rr$. |
| − | Any connected compact 1-manifold with non-empty boundary is homeomorphic to | + | * Any connected non-compact 1-manifold with non-empty boundary is homeomorphic to $\Rr_+$. |
| − | + | Thus for connected 1-manifolds two invariants, compactness and presence of boundary form a complete system of topological invariants. Each of the invariants takes two values. | |
| + | </wikitex> | ||
| − | + | ==== Remarks ==== | |
| + | <wikitex>; | ||
| + | Proofs of the results above are elementary. The core of them is the following simple | ||
| − | + | {{beginthm|Lemma}} Any connected 1-manifold covered by two open subsets homeomorphic to $\Rr$ is homeomorphic either to $\Rr$ or $S^1$.{{endthm}} | |
| − | The | + | The theorems above solve the topological classification problem for 1-manifolds in the most effective way that one can wish. Surprisingly, many Topology textbooks manage not to mention this fundamental result. |
| − | $\ | + | </wikitex> |
| + | === Corollaries === | ||
| + | ==== Homotopy classification of 1-manifolds ==== | ||
| + | <wikitex>; | ||
| + | Each connected 1-manifold is either contractible, or homotopy equivalent to circle. | ||
| + | </wikitex> | ||
| + | |||
| + | ==== 0-manifolds cobordant to zero ==== | ||
| + | <wikitex>; | ||
| + | A compact 0-manifold $X$ bounds a compact 1-manifold iff the number of points in $X$ is even. | ||
| + | </wikitex> | ||
| + | ==== Smooth structures ==== | ||
| + | <wikitex>; | ||
| + | ''Any 1-manifold admits a smooth structure.'' | ||
| + | |||
| + | If smooth 1-manifolds $X$ and $Y$ are homeomorphic, then they are also diffeomorphic. | ||
| + | Moreover, any homeomorphism $X\to Y$ can be approximated in the $C^0$-topology by a diffeomorphism. | ||
| + | |||
| + | Technically this can be considered as a corollary of the following simple theorem: | ||
| + | a map $\Rr\to\Rr$ is a homeomorphism iff it is a continuous monotone bijection. | ||
| + | </wikitex> | ||
| + | == Invariants == | ||
| + | |||
| + | <wikitex>; | ||
| + | As follows from the classification theorems, ''connectedness'', ''compactness'' and presence of ''boundary'' | ||
| + | play fundamental role in topology of 1-manifolds. Homotopy invariants are extremely simple. | ||
</wikitex> | </wikitex> | ||
== Further discussion == | == Further discussion == | ||
| + | ==== Connected sums ==== | ||
<wikitex>; | <wikitex>; | ||
| − | The | + | The very term ''connected sum'' is compromised in dimension 1. Indeed, a connected sum |
| + | of connected 1-manifolds may be not connected. For example a connected sum of two | ||
| + | copies of $\Rr$ is a disjoint sum of two copies of $\Rr$. | ||
| + | |||
| + | Moreover, connected sum, as an operation on topological types of 1-manifolds, is not well-defined. | ||
| + | Indeed, both $I\amalg\Rr$ and $\Rr_+\amalg\Rr_+$ can be presented as a connected sum of | ||
| + | two copies of $\Rr_+$. | ||
| + | |||
</wikitex> | </wikitex> | ||
| + | ==== Orientations ==== | ||
| + | <wikitex>; | ||
| + | Orientation of a 1-manifold can be interpreted as linear or cyclic orderings of their points. | ||
| + | An orientation of a connected non-closed 1-manifold is a | ||
| + | linear order on the set of its points such that the corresponding | ||
| + | interval topology coincides with the topology of this manifold. | ||
| + | |||
| + | An orientation of a connected closed 1-manifold is a | ||
| + | cyclic order on the set of its points such that the topology of this | ||
| + | cyclic order coincides with the topology of the 1-manifold. | ||
| + | |||
| + | An orientation of an arbitrary 1-manifold is a collection of orientations of its connected components (each component is equipped with an orientation). | ||
| + | |||
| + | Any 1-manifold admits an orientation. | ||
| + | |||
| + | Half-line $\Rr_+$ does not admit a homeomorphism reversing orientation. Any connected 1-manifold non-homeomorphic to $\Rr_+$ admits an orientation reversing map. | ||
| + | </wikitex> | ||
| + | |||
| + | ==== Mapping class groups ==== | ||
| + | <wikitex>; | ||
| + | |||
| + | </wikitex> | ||
| + | ==== Finite group actions ==== | ||
| + | <wikitex>; | ||
| + | |||
| + | </wikitex> | ||
| + | ==== Surgery ==== | ||
| + | <wikitex>; | ||
| + | |||
| + | </wikitex> | ||
== References == | == References == | ||
{{#RefList:}} | {{#RefList:}} | ||
Revision as of 05:25, 1 October 2009
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 08:32, 18 July 2013 and the changes since publication. |
Contents |
1 Introduction
According to the general definition of manifold, a manifold of dimension 1 is a topological space which is second countable (i.e., its topological structure has a countable base), satisfies the Hausdorff axiom (any two different points have disjoint neighborhoods) and each point of which has a neighborhood homeomorphic either to line 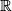 or half-line
or half-line 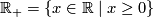 .
.
Manifolds of dimension 1 are called curves, but this name may lead to a confusion, because many mathematical objects share it. Even in the context of topology, the term curve may mean not only a manifold of dimension 1 with an additional structure, but, for instance, an immersion
of a smooth manifold of dimension 1 to Euclidean space 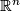 . To be on the safe side, we use an
unambiguous term manifold of dimension 1 or 1-manifold.
. To be on the safe side, we use an
unambiguous term manifold of dimension 1 or 1-manifold.
2 Examples
- Real line
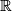
- Half-line
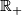
- Circle
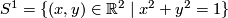
- Closed interval
![I=[0,1]](/images/math/1/c/a/1ca01533a825141b051c7492a6fa6427.png)
3 Classification
3.1 Reduction to classification of connected manifolds
Any manifold is homeomorphic to disjoint sum of its connected components.
A connected component of a 1-manifold is a 1-manifolds.
Two manifolds are homeomorphic iff there exists a one-to-one correspondence between their components such that the corresponding components are homeomorphic.
3.2 Topological classification of connected 1-manifolds
Theorem 3.1. Any connected 1-manifold is homeomorphic to one of the following 4 manifolds:
- real line
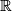
- half-line
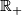
- circle
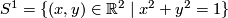
- closed interval
![I=[0,1]](/images/math/1/c/a/1ca01533a825141b051c7492a6fa6427.png) .
.
No two of these manifolds are homeomorphic to each other.
3.3 Characterizing the topological type of a connected 1-manifold
- Any connected closed 1-manifold is homeomorphic to
 .
.
- Any connected compact 1-manifold with non-empty boundary is homeomorphic to
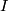 .
.
- Any connected non-compact 1-manifold without boundary is homeomorphic to
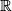 .
.
- Any connected non-compact 1-manifold with non-empty boundary is homeomorphic to
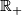 .
.
Thus for connected 1-manifolds two invariants, compactness and presence of boundary form a complete system of topological invariants. Each of the invariants takes two values.
3.4 Remarks
Proofs of the results above are elementary. The core of them is the following simple
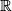 is homeomorphic either to
is homeomorphic either to 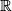 or
or  .
.The theorems above solve the topological classification problem for 1-manifolds in the most effective way that one can wish. Surprisingly, many Topology textbooks manage not to mention this fundamental result.
3.5 Corollaries
3.5.1 Homotopy classification of 1-manifolds
Each connected 1-manifold is either contractible, or homotopy equivalent to circle.
3.5.2 0-manifolds cobordant to zero
A compact 0-manifold  bounds a compact 1-manifold iff the number of points in
bounds a compact 1-manifold iff the number of points in  is even.
is even.
3.5.3 Smooth structures
Any 1-manifold admits a smooth structure.
If smooth 1-manifolds  and
and  are homeomorphic, then they are also diffeomorphic.
Moreover, any homeomorphism
are homeomorphic, then they are also diffeomorphic.
Moreover, any homeomorphism 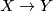 can be approximated in the
can be approximated in the 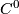 -topology by a diffeomorphism.
-topology by a diffeomorphism.
Technically this can be considered as a corollary of the following simple theorem:
a map 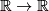 is a homeomorphism iff it is a continuous monotone bijection.
is a homeomorphism iff it is a continuous monotone bijection.
4 Invariants
As follows from the classification theorems, connectedness, compactness and presence of boundary play fundamental role in topology of 1-manifolds. Homotopy invariants are extremely simple.
5 Further discussion
5.1 Connected sums
The very term connected sum is compromised in dimension 1. Indeed, a connected sum
of connected 1-manifolds may be not connected. For example a connected sum of two
copies of 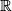 is a disjoint sum of two copies of
is a disjoint sum of two copies of 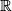 .
.
Moreover, connected sum, as an operation on topological types of 1-manifolds, is not well-defined.
Indeed, both  and
and 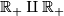 can be presented as a connected sum of
two copies of
can be presented as a connected sum of
two copies of 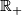 .
.
5.2 Orientations
Orientation of a 1-manifold can be interpreted as linear or cyclic orderings of their points.
An orientation of a connected non-closed 1-manifold is a linear order on the set of its points such that the corresponding interval topology coincides with the topology of this manifold.
An orientation of a connected closed 1-manifold is a cyclic order on the set of its points such that the topology of this cyclic order coincides with the topology of the 1-manifold.
An orientation of an arbitrary 1-manifold is a collection of orientations of its connected components (each component is equipped with an orientation).
Any 1-manifold admits an orientation.
Half-line 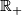 does not admit a homeomorphism reversing orientation. Any connected 1-manifold non-homeomorphic to
does not admit a homeomorphism reversing orientation. Any connected 1-manifold non-homeomorphic to 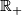 admits an orientation reversing map.
admits an orientation reversing map.
5.3 Mapping class groups
5.4 Finite group actions
5.5 Surgery
6 References
|
This page has not been refereed. The information given here might be incomplete or provisional. |