Manifolds with singularities
Contents |
1 Introduction
Manifolds with singularities are geometric objects in topology generalizing manifolds. They were introduced in ([Sullivan1996],[Sullivan1967]) and [Baas1973]. Applications of the concept include representing cycles in homology theories with coefficients.
2 Definitions
2.1 Cone-like singularities
A manifold with singularities of Baas-Sullivan type is a topological space 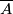 that looks like a manifold outside of a compact 'singularity set', while the singularity set has a neighborhood that looks like the product of manifold and a cone.
Here is a precise definition. Let
that looks like a manifold outside of a compact 'singularity set', while the singularity set has a neighborhood that looks like the product of manifold and a cone.
Here is a precise definition. Let  be a closed manifold. A manifold with a
be a closed manifold. A manifold with a  -singularity (following [Baas1973]) is a space of the form
-singularity (following [Baas1973]) is a space of the form
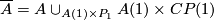
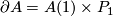
Here,  is a manifold with boundary
is a manifold with boundary 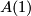 .
.
2.2  -manifolds
-manifolds
Following ([Botvinnik2001], [Botvinnik1992]), a more general definition can be given. Let  be a (possibly empty) collection of closed manifolds and denote by
be a (possibly empty) collection of closed manifolds and denote by 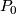 the set containing only one point. Then define
the set containing only one point. Then define 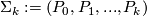 . For a subset
. For a subset 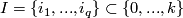 define
define 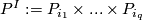 .
.
Definition 2.1.A manifold  is a
is a  -Manifold if
-Manifold if
- there is a partition
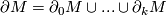 , such that
, such that 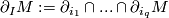 is a manifold for each
is a manifold for each 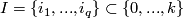 , and such that
, and such that
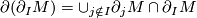
- for each
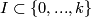 there is a manifold
there is a manifold 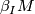 and a diffeomorphism
and a diffeomorphism
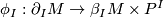
such that if  and
and 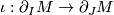 is the inclusion, then the composition
is the inclusion, then the composition
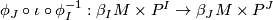
restricts to the identity on the factor 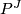 in
in 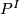 . The diffeomorphisms
. The diffeomorphisms 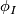 are called product structures.
are called product structures.
On a  -manifold
-manifold  , there is a canonical equivalence relation
, there is a canonical equivalence relation 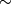 : two points
: two points 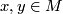 are defined to be equivalent if there is an
are defined to be equivalent if there is an 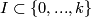 such that
such that 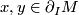 and
and 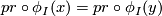 , where
, where 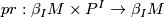 is the projection.
Now we can give a general definition: a manifold with a
is the projection.
Now we can give a general definition: a manifold with a  -singularity is a topological space
-singularity is a topological space 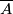 of the form
of the form
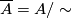
for a  -manifold
-manifold  .
.
The spaces defined above as manifolds with a  -singularity are contained in this more general definition. In fact, they give the manifolds with a
-singularity are contained in this more general definition. In fact, they give the manifolds with a 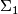 -singularity. For given a manifold
-singularity. For given a manifold  , set
, set 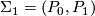 . Then the manifold
. Then the manifold  with boundary
with boundary 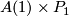 , which appears in the above definition, is a
, which appears in the above definition, is a 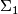 -manifold. The attachement of the cone-end
-manifold. The attachement of the cone-end 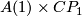 now corresponds to the collapsing of the equivalence relation
now corresponds to the collapsing of the equivalence relation 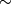 in
in  .
.
3 Some examples
3.1 Intersecting spheres
A basic example is presented by two spheres intersecting each other in a sphere of lower dimension. Choose an embedding 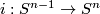 . Then define
. Then define 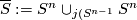 . Outside of the intersecting sphere
. Outside of the intersecting sphere 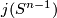 this is an
this is an  -dimensional manifold. The intersecting sphere itself has a neigborhood homeomorphic to the product of
-dimensional manifold. The intersecting sphere itself has a neigborhood homeomorphic to the product of 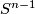 and a cone over
and a cone over 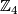 . We can write
. We can write 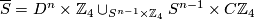 .
.
3.2 Inverse images of critical points
Let 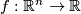 be a Morse-function with
be a Morse-function with  as a single critical point. We can suppose that
as a single critical point. We can suppose that 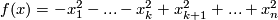 near
near  . Setting
. Setting 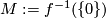 , we see that the cone
, we see that the cone 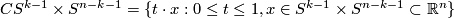 provides a neighborhood of
provides a neighborhood of  in
in  . It follows that
. It follows that  is of the form $
is of the form $
4 Invariants
...
5 Classification/Characterization
...
6 Further discussion
...
7 References
- [Baas1973] N. A. Baas, On bordism theory of manifolds with singularities, Math. Scand. 33 (1973), 279–302 (1974). MR0346824 (49 #11547b) Zbl 0281.57027
- [Botvinnik1992] B. I. Botvinnik, Manifolds with singularities and the Adams-Novikov spectral sequence, Cambridge University Press, Cambridge, 1992. MR1192127 (93h:55002) Zbl 0764.55001
- [Botvinnik2001] B. Botvinnik, Manifolds with singularities accepting a metric of positive scalar curvature, Geom. Topol. 5 (2001), 683–718 (electronic). MR1857524 (2002j:57045) Zbl 1002.57055
- [Sullivan1967] D. Sullivan, On the Hauptvermutung for manifolds, Bull. Amer. Math. Soc. 73 (1967), 598–600. MR0212811 (35 #3676) Zbl 0153.54002
- [Sullivan1996] D. P. Sullivan, Triangulating and smoothing homotopy equivalences and homeomorphisms. Geometric Topology Seminar Notes, 1 (1996), 69–103. MR1434103 (98c:57027) Zbl 0871.57021
|
This page has not been refereed. The information given here might be incomplete or provisional. |
 be a closed manifold. A manifold with a
be a closed manifold. A manifold with a  -singularity (following [Baas1973]) is a space of the form
-singularity (following [Baas1973]) is a space of the form
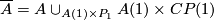
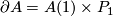
Here,  is a manifold with boundary
is a manifold with boundary 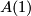 .
.
2.2  -manifolds
-manifolds
Following ([Botvinnik2001], [Botvinnik1992]), a more general definition can be given. Let  be a (possibly empty) collection of closed manifolds and denote by
be a (possibly empty) collection of closed manifolds and denote by 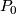 the set containing only one point. Then define
the set containing only one point. Then define 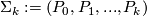 . For a subset
. For a subset 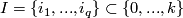 define
define 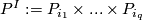 .
.
Definition 2.1.A manifold  is a
is a  -Manifold if
-Manifold if
- there is a partition
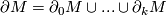 , such that
, such that 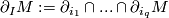 is a manifold for each
is a manifold for each 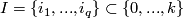 , and such that
, and such that
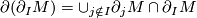
- for each
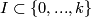 there is a manifold
there is a manifold 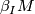 and a diffeomorphism
and a diffeomorphism
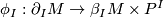
such that if  and
and 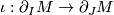 is the inclusion, then the composition
is the inclusion, then the composition
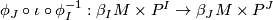
restricts to the identity on the factor 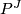 in
in 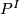 . The diffeomorphisms
. The diffeomorphisms 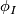 are called product structures.
are called product structures.
On a  -manifold
-manifold  , there is a canonical equivalence relation
, there is a canonical equivalence relation 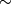 : two points
: two points 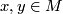 are defined to be equivalent if there is an
are defined to be equivalent if there is an 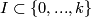 such that
such that 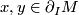 and
and 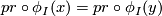 , where
, where 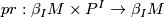 is the projection.
Now we can give a general definition: a manifold with a
is the projection.
Now we can give a general definition: a manifold with a  -singularity is a topological space
-singularity is a topological space 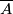 of the form
of the form
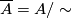
for a  -manifold
-manifold  .
.
The spaces defined above as manifolds with a  -singularity are contained in this more general definition. In fact, they give the manifolds with a
-singularity are contained in this more general definition. In fact, they give the manifolds with a 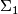 -singularity. For given a manifold
-singularity. For given a manifold  , set
, set 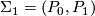 . Then the manifold
. Then the manifold  with boundary
with boundary 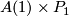 , which appears in the above definition, is a
, which appears in the above definition, is a 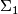 -manifold. The attachement of the cone-end
-manifold. The attachement of the cone-end 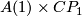 now corresponds to the collapsing of the equivalence relation
now corresponds to the collapsing of the equivalence relation 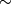 in
in  .
.
3 Some examples
3.1 Intersecting spheres
A basic example is presented by two spheres intersecting each other in a sphere of lower dimension. Choose an embedding 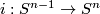 . Then define
. Then define 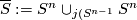 . Outside of the intersecting sphere
. Outside of the intersecting sphere 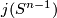 this is an
this is an  -dimensional manifold. The intersecting sphere itself has a neigborhood homeomorphic to the product of
-dimensional manifold. The intersecting sphere itself has a neigborhood homeomorphic to the product of 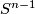 and a cone over
and a cone over 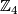 . We can write
. We can write 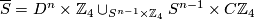 .
.
3.2 Inverse images of critical points
Let 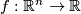 be a Morse-function with
be a Morse-function with  as a single critical point. We can suppose that
as a single critical point. We can suppose that 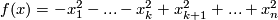 near
near  . Setting
. Setting 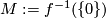 , we see that the cone
, we see that the cone 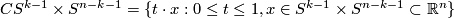 provides a neighborhood of
provides a neighborhood of  in
in  . It follows that
. It follows that  is of the form $
is of the form $
4 Invariants
...
5 Classification/Characterization
...
6 Further discussion
...
7 References
- [Baas1973] N. A. Baas, On bordism theory of manifolds with singularities, Math. Scand. 33 (1973), 279–302 (1974). MR0346824 (49 #11547b) Zbl 0281.57027
- [Botvinnik1992] B. I. Botvinnik, Manifolds with singularities and the Adams-Novikov spectral sequence, Cambridge University Press, Cambridge, 1992. MR1192127 (93h:55002) Zbl 0764.55001
- [Botvinnik2001] B. Botvinnik, Manifolds with singularities accepting a metric of positive scalar curvature, Geom. Topol. 5 (2001), 683–718 (electronic). MR1857524 (2002j:57045) Zbl 1002.57055
- [Sullivan1967] D. Sullivan, On the Hauptvermutung for manifolds, Bull. Amer. Math. Soc. 73 (1967), 598–600. MR0212811 (35 #3676) Zbl 0153.54002
- [Sullivan1996] D. P. Sullivan, Triangulating and smoothing homotopy equivalences and homeomorphisms. Geometric Topology Seminar Notes, 1 (1996), 69–103. MR1434103 (98c:57027) Zbl 0871.57021
|
This page has not been refereed. The information given here might be incomplete or provisional. |
 be a closed manifold. A manifold with a
be a closed manifold. A manifold with a  -singularity (following [Baas1973]) is a space of the form
-singularity (following [Baas1973]) is a space of the form
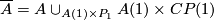
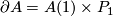
Here,  is a manifold with boundary
is a manifold with boundary 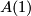 .
.
2.2  -manifolds
-manifolds
Following ([Botvinnik2001], [Botvinnik1992]), a more general definition can be given. Let  be a (possibly empty) collection of closed manifolds and denote by
be a (possibly empty) collection of closed manifolds and denote by 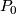 the set containing only one point. Then define
the set containing only one point. Then define 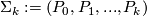 . For a subset
. For a subset 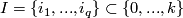 define
define 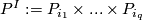 .
.
Definition 2.1.A manifold  is a
is a  -Manifold if
-Manifold if
- there is a partition
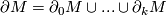 , such that
, such that 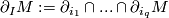 is a manifold for each
is a manifold for each 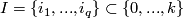 , and such that
, and such that
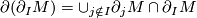
- for each
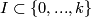 there is a manifold
there is a manifold 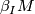 and a diffeomorphism
and a diffeomorphism
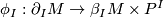
such that if  and
and 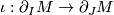 is the inclusion, then the composition
is the inclusion, then the composition
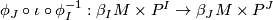
restricts to the identity on the factor 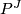 in
in 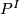 . The diffeomorphisms
. The diffeomorphisms 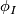 are called product structures.
are called product structures.
On a  -manifold
-manifold  , there is a canonical equivalence relation
, there is a canonical equivalence relation 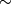 : two points
: two points 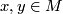 are defined to be equivalent if there is an
are defined to be equivalent if there is an 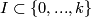 such that
such that 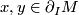 and
and 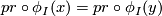 , where
, where 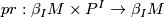 is the projection.
Now we can give a general definition: a manifold with a
is the projection.
Now we can give a general definition: a manifold with a  -singularity is a topological space
-singularity is a topological space 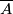 of the form
of the form
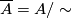
for a  -manifold
-manifold  .
.
The spaces defined above as manifolds with a  -singularity are contained in this more general definition. In fact, they give the manifolds with a
-singularity are contained in this more general definition. In fact, they give the manifolds with a 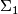 -singularity. For given a manifold
-singularity. For given a manifold  , set
, set 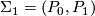 . Then the manifold
. Then the manifold  with boundary
with boundary 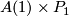 , which appears in the above definition, is a
, which appears in the above definition, is a 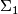 -manifold. The attachement of the cone-end
-manifold. The attachement of the cone-end 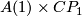 now corresponds to the collapsing of the equivalence relation
now corresponds to the collapsing of the equivalence relation 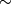 in
in  .
.
3 Some examples
3.1 Intersecting spheres
A basic example is presented by two spheres intersecting each other in a sphere of lower dimension. Choose an embedding 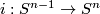 . Then define
. Then define 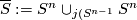 . Outside of the intersecting sphere
. Outside of the intersecting sphere 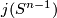 this is an
this is an  -dimensional manifold. The intersecting sphere itself has a neigborhood homeomorphic to the product of
-dimensional manifold. The intersecting sphere itself has a neigborhood homeomorphic to the product of 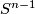 and a cone over
and a cone over 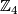 . We can write
. We can write 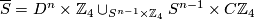 .
.
3.2 Inverse images of critical points
Let 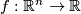 be a Morse-function with
be a Morse-function with  as a single critical point. We can suppose that
as a single critical point. We can suppose that 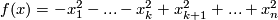 near
near  . Setting
. Setting 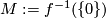 , we see that the cone
, we see that the cone 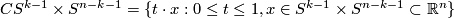 provides a neighborhood of
provides a neighborhood of  in
in  . It follows that
. It follows that  is of the form $
is of the form $
4 Invariants
...
5 Classification/Characterization
...
6 Further discussion
...
7 References
- [Baas1973] N. A. Baas, On bordism theory of manifolds with singularities, Math. Scand. 33 (1973), 279–302 (1974). MR0346824 (49 #11547b) Zbl 0281.57027
- [Botvinnik1992] B. I. Botvinnik, Manifolds with singularities and the Adams-Novikov spectral sequence, Cambridge University Press, Cambridge, 1992. MR1192127 (93h:55002) Zbl 0764.55001
- [Botvinnik2001] B. Botvinnik, Manifolds with singularities accepting a metric of positive scalar curvature, Geom. Topol. 5 (2001), 683–718 (electronic). MR1857524 (2002j:57045) Zbl 1002.57055
- [Sullivan1967] D. Sullivan, On the Hauptvermutung for manifolds, Bull. Amer. Math. Soc. 73 (1967), 598–600. MR0212811 (35 #3676) Zbl 0153.54002
- [Sullivan1996] D. P. Sullivan, Triangulating and smoothing homotopy equivalences and homeomorphisms. Geometric Topology Seminar Notes, 1 (1996), 69–103. MR1434103 (98c:57027) Zbl 0871.57021
|
This page has not been refereed. The information given here might be incomplete or provisional. |
 be a closed manifold. A manifold with a
be a closed manifold. A manifold with a  -singularity (following [Baas1973]) is a space of the form
-singularity (following [Baas1973]) is a space of the form
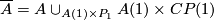
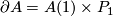
Here,  is a manifold with boundary
is a manifold with boundary 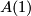 .
.
2.2  -manifolds
-manifolds
Following ([Botvinnik2001], [Botvinnik1992]), a more general definition can be given. Let  be a (possibly empty) collection of closed manifolds and denote by
be a (possibly empty) collection of closed manifolds and denote by 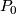 the set containing only one point. Then define
the set containing only one point. Then define 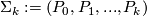 . For a subset
. For a subset 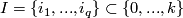 define
define 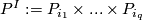 .
.
Definition 2.1.A manifold  is a
is a  -Manifold if
-Manifold if
- there is a partition
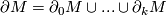 , such that
, such that 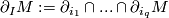 is a manifold for each
is a manifold for each 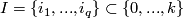 , and such that
, and such that
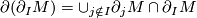
- for each
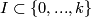 there is a manifold
there is a manifold 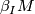 and a diffeomorphism
and a diffeomorphism
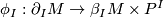
such that if  and
and 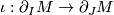 is the inclusion, then the composition
is the inclusion, then the composition
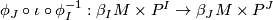
restricts to the identity on the factor 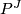 in
in 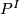 . The diffeomorphisms
. The diffeomorphisms 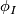 are called product structures.
are called product structures.
On a  -manifold
-manifold  , there is a canonical equivalence relation
, there is a canonical equivalence relation 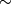 : two points
: two points 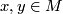 are defined to be equivalent if there is an
are defined to be equivalent if there is an 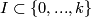 such that
such that 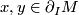 and
and 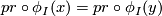 , where
, where 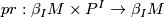 is the projection.
Now we can give a general definition: a manifold with a
is the projection.
Now we can give a general definition: a manifold with a  -singularity is a topological space
-singularity is a topological space 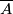 of the form
of the form
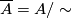
for a  -manifold
-manifold  .
.
The spaces defined above as manifolds with a  -singularity are contained in this more general definition. In fact, they give the manifolds with a
-singularity are contained in this more general definition. In fact, they give the manifolds with a 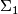 -singularity. For given a manifold
-singularity. For given a manifold  , set
, set 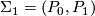 . Then the manifold
. Then the manifold  with boundary
with boundary 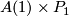 , which appears in the above definition, is a
, which appears in the above definition, is a 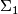 -manifold. The attachement of the cone-end
-manifold. The attachement of the cone-end 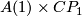 now corresponds to the collapsing of the equivalence relation
now corresponds to the collapsing of the equivalence relation 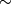 in
in  .
.
3 Some examples
3.1 Intersecting spheres
A basic example is presented by two spheres intersecting each other in a sphere of lower dimension. Choose an embedding 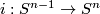 . Then define
. Then define 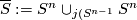 . Outside of the intersecting sphere
. Outside of the intersecting sphere 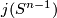 this is an
this is an  -dimensional manifold. The intersecting sphere itself has a neigborhood homeomorphic to the product of
-dimensional manifold. The intersecting sphere itself has a neigborhood homeomorphic to the product of 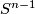 and a cone over
and a cone over 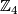 . We can write
. We can write 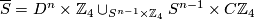 .
.
3.2 Inverse images of critical points
Let 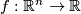 be a Morse-function with
be a Morse-function with  as a single critical point. We can suppose that
as a single critical point. We can suppose that 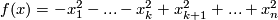 near
near  . Setting
. Setting 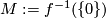 , we see that the cone
, we see that the cone 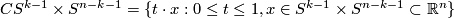 provides a neighborhood of
provides a neighborhood of  in
in  . It follows that
. It follows that  is of the form $
is of the form $
4 Invariants
...
5 Classification/Characterization
...
6 Further discussion
...
7 References
- [Baas1973] N. A. Baas, On bordism theory of manifolds with singularities, Math. Scand. 33 (1973), 279–302 (1974). MR0346824 (49 #11547b) Zbl 0281.57027
- [Botvinnik1992] B. I. Botvinnik, Manifolds with singularities and the Adams-Novikov spectral sequence, Cambridge University Press, Cambridge, 1992. MR1192127 (93h:55002) Zbl 0764.55001
- [Botvinnik2001] B. Botvinnik, Manifolds with singularities accepting a metric of positive scalar curvature, Geom. Topol. 5 (2001), 683–718 (electronic). MR1857524 (2002j:57045) Zbl 1002.57055
- [Sullivan1967] D. Sullivan, On the Hauptvermutung for manifolds, Bull. Amer. Math. Soc. 73 (1967), 598–600. MR0212811 (35 #3676) Zbl 0153.54002
- [Sullivan1996] D. P. Sullivan, Triangulating and smoothing homotopy equivalences and homeomorphisms. Geometric Topology Seminar Notes, 1 (1996), 69–103. MR1434103 (98c:57027) Zbl 0871.57021
|
This page has not been refereed. The information given here might be incomplete or provisional. |