Simple closed curves in surfaces (Ex)

Let $\Sigma_g$$\newcommand{\Z}{\mathbb{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\F}{\mathbb{F}} \newcommand{\bZ}{\mathbb{Z}} \newcommand{\bR}{\mathbb{R}} \newcommand{\bC}{\mathbb{C}} \newcommand{\bH}{\mathbb{H}} \newcommand{\bQ}{\mathbb{Q}} \newcommand{\bF}{\mathbb{F}} \newcommand{\bN}{\mathbb{N}} \DeclareMathOperator\id{id} % identity map \DeclareMathOperator\Sq{Sq} % Steenrod squares \DeclareMathOperator\Homeo{Homeo} % group of homeomorphisms of a topoloical space \DeclareMathOperator\Diff{Diff} % group of diffeomorphisms of a smooth manifold \DeclareMathOperator\SDiff{SDiff} % diffeomorphism under some constraint \DeclareMathOperator\Hom{Hom} % homomrphism group \DeclareMathOperator\End{End} % endomorphism group \DeclareMathOperator\Aut{Aut} % automorphism group \DeclareMathOperator\Inn{Inn} % inner automorphisms \DeclareMathOperator\Out{Out} % outer automorphism group \DeclareMathOperator\vol{vol} % volume \newcommand{\GL}{\text{GL}} % general linear group \newcommand{\SL}{\text{SL}} % special linear group \newcommand{\SO}{\text{SO}} % special orthogonal group \newcommand{\O}{\text{O}} % orthogonal group \newcommand{\SU}{\text{SU}} % special unitary group \newcommand{\Spin}{\text{Spin}} % Spin group \newcommand{\RP}{\Rr\mathrm P} % real projective space \newcommand{\CP}{\Cc\mathrm P} % complex projective space \newcommand{\HP}{\Hh\mathrm P} % quaternionic projective space \newcommand{\Top}{\mathrm{Top}} % topological category \newcommand{\PL}{\mathrm{PL}} % piecewise linear category \newcommand{\Cat}{\mathrm{Cat}} % any category \newcommand{\KS}{\text{KS}} % Kirby-Siebenmann class \newcommand{\Hud}{\text{Hud}} % Hudson torus \newcommand{\Ker}{\text{Ker}} % Kernel \newcommand{\underbar}{\underline} %Classifying Spaces for Families of Subgroups \newcommand{\textup}{\text} \newcommand{\sp}{^}\Sigma_g$ 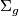be a closed oriented surface of genus $g$$g$ and let $\alpha_1, \dots, \alpha_g \subset \Sigma_g$$\alpha_1, \dots, \alpha_g \subset \Sigma_g$ 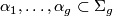be pair-wise disjoint simple closed curves. 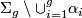Prove that the homology classes $\{[\alpha_1], \dots [\alpha_g]\} \subset H_1(\Sigma_g; \Z/2)$$\{[\alpha_1], \dots [\alpha_g]\} \subset H_1(\Sigma_g; \Z/2)$ are linearly independent if the complement $\Sigma_g \setminus \cup_{i=1}^g \alpha_i$$\Sigma_g \setminus \cup_{i=1}^g \alpha_i$ is connected.