Talk:Structured chain complexes IV (Ex)
From Manifold Atlas
Recall the suspension maps
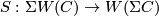
where  can mean
can mean 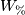 ,
, 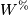 , or
, or 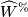 defined in TM L-Theory II. We wish to compute
defined in TM L-Theory II. We wish to compute
Tex syntax error
Consider the exact sequence
![\displaystyle \xymatrix{ 0 \ar[r] & W^{\%}(C) \ar[r] & \widehat{W}^{\%}(C) \ar[r] & \Sigma W_{\%} (C) \ar[r] & 0 }](/images/math/7/4/5/74570104f3c5529e71741f33e7078c58.png)
By functoriality, we get maps 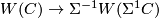 for all different brands of
for all different brands of  , and these are the maps that represent the above colimit. These maps induce a diagram
, and these are the maps that represent the above colimit. These maps induce a diagram
![\displaystyle \xymatrix{ 0 \ar[r] & W^{\%}(C) \ar[d] \ar[r] & \widehat{W}^{\%} \ar[r] \ar[d] & \Sigma W_{\%}(C) \ar[d] \ar[r] & 0 \\ 0 \ar[r] & \Sigma^{-k} W^{\%}(\Sigma^k C) \ar[r] & \Sigma^{-k}\widehat{W}^{\%}(\Sigma^k C) \ar[r] & \Sigma^{-k+1} W_{\%}(\Sigma^k C) \ar[r] & 0 . \\ }](/images/math/2/0/7/207c69825c11dcc92576815d3cfae99c.png)
We have seen that the suspension map
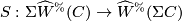
is a homotopy equivalence. Iterating this we see hocolim 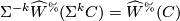 .
.
Now, note that for chain complexes 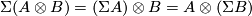 . Thus
. Thus
![\displaystyle \Sigma^{-k} W_{\%}(\Sigma^k C) \simeq \Sigma^k(W \otimes_{\mathbb{Z}[\mathbb{Z}/2]} (C \otimes C))](/images/math/8/4/6/84636dcbe2bca9efb3d2f3034cfe43b1.png)
This complex increases linearly in connectivity as  increases, hence its homotopy colimit is contractible. That is
increases, hence its homotopy colimit is contractible. That is
Tex syntax error
By exactness of the short exact sequences in our diagram, and the remarks above, we conclude that
Tex syntax error