Talk:Normal bundles in products of spheres (Ex)
1. The normal bundle of the diagonal embedding 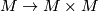 is isomorphic to the tangent bundle of
is isomorphic to the tangent bundle of  . The tangent bundle of
. The tangent bundle of 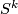 is trivial if and only if
is trivial if and only if 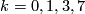 , by Adam's theorem.
, by Adam's theorem.
2. We present two solutions.
Low-tech solution: Given immersions 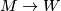 and
and 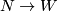 of closed manifolds, one can produce an immersion
of closed manifolds, one can produce an immersion 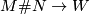 by "connecting the immersions by a tube". (See for instance the definition of the sum in
by "connecting the immersions by a tube". (See for instance the definition of the sum in 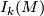 in Lück's book.) If both immersions happen to have a trivial normal bundle, then the immersion
in Lück's book.) If both immersions happen to have a trivial normal bundle, then the immersion 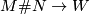 also has a trivial normal bundle.
also has a trivial normal bundle.
We use this for 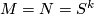 and
and 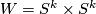 , where the first immersion is the inclusion
, where the first immersion is the inclusion 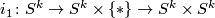 and the second one is the corresponding inclusion
and the second one is the corresponding inclusion 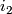 into the second factor. Both these embeddings apparently have trivial normal bundles. Hence so does their "sum"
into the second factor. Both these embeddings apparently have trivial normal bundles. Hence so does their "sum"
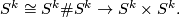
The homotopy class of this map is given by 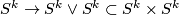 where the first map is the pinch map. By definition of the sum in
where the first map is the pinch map. By definition of the sum in 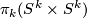 , it is thus the sum
, it is thus the sum 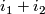 . Its Hurewicz image is given by the diagonal class
. Its Hurewicz image is given by the diagonal class 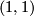 .
.
High-tech solution: The Hirsch-Smale classification of immersions implies that
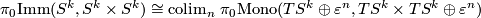
where 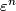 denotes the
denotes the  -dimensional trivial bundle.
-dimensional trivial bundle.
We will use surjectivity. Both the bundles 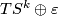 and
and 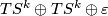 over
over 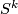 are trivial, thus isomorphic to
are trivial, thus isomorphic to 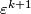 and
and 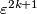 respectively. However the inclusion
respectively. However the inclusion 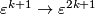 of the first
of the first  summands is a bundle monomorphism with trivial complement.
summands is a bundle monomorphism with trivial complement.
By Smale-Hirsch, the homotopy class of the composite
![\displaystyle \xymatrix{ TS^k \oplus \varepsilon \ar[r] \ar[d] & TS^k \oplus TS^k \oplus \varepsilon \ar[r]\ar[d] & (TS^k \times TS^k) \oplus \varepsilon \ar[d]\\ S^k \ar[r]^{\mathrm{id}} & S^k \ar[r]^{\Delta} & S^k\times S^k }](/images/math/2/0/2/2028683a826ea5b74f0ce403a345800d.png)
is the differential of an immersion.
Its normal bundle is still trivial. Moreover, by construction, this immersion is (non-regularly) homotopic to the diagonal. So its Hurewicz image is the diagonal class 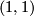 .
.