Talk:K-group, first (Ex)

First we show that the determinant induces a well-defined morphism

$\displaystyle \xymatrix{\det:K_1( R) \ar[r] & R^\times.}$

For this we recall that 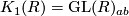$K_1( R) = \mathrm{GL}( R)_{ab}$$\newcommand{\Z}{\mathbb{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\F}{\mathbb{F}} \newcommand{\bZ}{\mathbb{Z}} \newcommand{\bR}{\mathbb{R}} \newcommand{\bC}{\mathbb{C}} \newcommand{\bH}{\mathbb{H}} \newcommand{\bQ}{\mathbb{Q}} \newcommand{\bF}{\mathbb{F}} \newcommand{\bN}{\mathbb{N}} \DeclareMathOperator\id{id} % identity map \DeclareMathOperator\Sq{Sq} % Steenrod squares \DeclareMathOperator\Homeo{Homeo} % group of homeomorphisms of a topoloical space \DeclareMathOperator\Diff{Diff} % group of diffeomorphisms of a smooth manifold \DeclareMathOperator\SDiff{SDiff} % diffeomorphism under some constraint \DeclareMathOperator\Hom{Hom} % homomrphism group \DeclareMathOperator\End{End} % endomorphism group \DeclareMathOperator\Aut{Aut} % automorphism group \DeclareMathOperator\Inn{Inn} % inner automorphisms \DeclareMathOperator\Out{Out} % outer automorphism group \DeclareMathOperator\vol{vol} % volume \newcommand{\GL}{\text{GL}} % general linear group \newcommand{\SL}{\text{SL}} % special linear group \newcommand{\SO}{\text{SO}} % special orthogonal group \newcommand{\O}{\text{O}} % orthogonal group \newcommand{\SU}{\text{SU}} % special unitary group \newcommand{\Spin}{\text{Spin}} % Spin group \newcommand{\RP}{\Rr\mathrm P} % real projective space \newcommand{\CP}{\Cc\mathrm P} % complex projective space \newcommand{\HP}{\Hh\mathrm P} % quaternionic projective space \newcommand{\Top}{\mathrm{Top}} % topological category \newcommand{\PL}{\mathrm{PL}} % piecewise linear category \newcommand{\Cat}{\mathrm{Cat}} % any category \newcommand{\KS}{\text{KS}} % Kirby-Siebenmann class \newcommand{\Hud}{\text{Hud}} % Hudson torus \newcommand{\Ker}{\text{Ker}} % Kernel \newcommand{\underbar}{\underline} %Classifying Spaces for Families of Subgroups \newcommand{\textup}{\text} \newcommand{\sp}{^}K_1( R) = \mathrm{GL}( R)_{ab}$ is the abelianization of the infinite general linear group over $R$$R$. 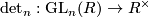Surely, since the ring is commutative, for every $n$$n$ we have the determinat as a map $\det_n: \mathrm{GL}_n( R) \to R^\times$$\det_n: \mathrm{GL}_n( R) \to R^\times$ and the diagram

$\displaystyle \xymatrix{ \mathrm{GL}_n( R) \ar[r]^-{\det_n} \ar[d]_\iota & R^\times \\ \mathrm{GL}_{n+1}( R) \ar@/_1.3pc/[ur]_-{\det_{n+1}} & }$

commutes, where $\iota$$\iota$ is the canonical inclusion as block matrix in the upper left corner.

Hence we get a well-defined map on the colimit 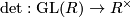$\det: \mathrm{GL}( R) \to R^\times$$\det: \mathrm{GL}( R) \to R^\times$ by standard properties of the determinant we see that this map factors over the abelianization to obtain the desired map

$\displaystyle \xymatrix{\det: K_1( R) \ar[r] & R^\times.}$

The fact that this map is surjective follows from the easy observation that we have the canonical map

$\displaystyle R^\times = \mathrm{GL}_1( R) \to K_1( R)$ $$\displaystyle R^\times = \mathrm{GL}_1( R) \to K_1( R)$$

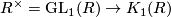
which obviously splits the determinant.