Talk:Homotopy spheres II (Ex)
Exercise 3.
Suppose that 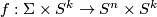 is a diffeomorphism. Then
is a diffeomorphism. Then 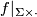 is an embedding of
is an embedding of  into
into 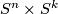 with trivial normal bundle. Therefore the composition of
with trivial normal bundle. Therefore the composition of 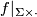 with the standard embedding
with the standard embedding 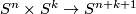 is an embedding
is an embedding 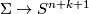 with trivial normal bundle.
with trivial normal bundle.
Now assume that there is an embedding of  into
into 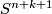 with trivial normal bundle. Consider the tubular neighborhood of
with trivial normal bundle. Consider the tubular neighborhood of  in
in 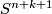 . Its boundary is
. Its boundary is 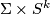 embedded into
embedded into 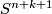 .
.
Denote by  the "interior" connected component of
the "interior" connected component of 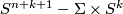 , i.e. the component homeomorphic to
, i.e. the component homeomorphic to 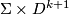 . Let
. Let 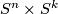 be standardly embedded into
be standardly embedded into 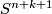 and disjoint with
and disjoint with 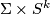 . Denote by
. Denote by  the "exterior" connected component of
the "exterior" connected component of 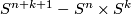 , i.e. the component homeomorphic to
, i.e. the component homeomorphic to 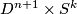 .
.
Then 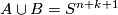 and
and 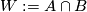 is a manifold with boundary
is a manifold with boundary 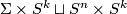 . Using Mayer–Vietoris sequence for
. Using Mayer–Vietoris sequence for 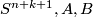 we obtain that the homologies of
we obtain that the homologies of  equal to the homologies of
equal to the homologies of 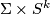 (or
(or 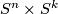 ) and that inclusions
) and that inclusions 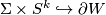 and
and 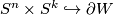 induce isomorphism in homologies. Since both
induce isomorphism in homologies. Since both 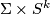 and
and 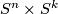 are simply-connected then these inclusions are homotopy equivalences.
are simply-connected then these inclusions are homotopy equivalences.
So,  is an
is an  -cobordism. Therefore since
-cobordism. Therefore since 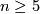 then
then  -cobordism Theorem implies that
-cobordism Theorem implies that 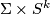 is diffeomorphic to
is diffeomorphic to 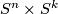 .
.