Talk:Fundamental groups of surfaces (Ex)
From Manifold Atlas
Let  be a surface. Suppose
be a surface. Suppose 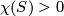 . Then
. Then 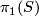 is finite and hence hyperbolic.
is finite and hence hyperbolic.
Suppose 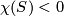 . Then the interior of
. Then the interior of  is a quotient of
is a quotient of 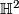 by a discrete torsion-free subgroup
by a discrete torsion-free subgroup 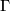 of
of 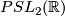 . Then
. Then 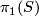 is hyperbolic since it is isomorphic to
is hyperbolic since it is isomorphic to 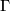 which acts freely and properly discontinuously on
which acts freely and properly discontinuously on 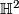 .
.
Now let 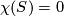 . If
. If  has boundary, then it is homeomorphic to an annulus or a Mobius band. Each of which have fundamental group
has boundary, then it is homeomorphic to an annulus or a Mobius band. Each of which have fundamental group  which is hyperbolic since its Cayley graph is quasi-isometric to a tree.
which is hyperbolic since its Cayley graph is quasi-isometric to a tree.
The only remaining cases are the Klein bottle and the torus. The latter has fundamental group 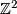 , while the fundamental group of the former contains
, while the fundamental group of the former contains 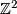 as an index 2 subgroup. Thus neither of these groups is hyperbolic.
as an index 2 subgroup. Thus neither of these groups is hyperbolic.