Talk:Connected sum of topological manifolds (Ex)
Part 1
Let 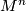 be an (oriented) topological
be an (oriented) topological  -manifold. Choose any two locally flat embeddings
-manifold. Choose any two locally flat embeddings 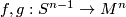 so that
so that 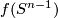 and
and 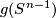 bound topological balls in
bound topological balls in 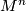 . We will show that
. We will show that 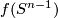 is topologically isotopic to
is topologically isotopic to 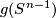 . This fact implies that connected sum of topological manifolds is well-defined, as the connected sum of
. This fact implies that connected sum of topological manifolds is well-defined, as the connected sum of 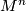 and
and 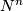 can then be defined by deleting a topological ball from each and then gluing the boundary, respecting the orientations on
can then be defined by deleting a topological ball from each and then gluing the boundary, respecting the orientations on 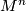 and
and 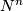 (the gluing map is determined up to homotopy by the orientations, as an orientation-preserving automorphism of
(the gluing map is determined up to homotopy by the orientations, as an orientation-preserving automorphism of 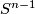 . We will show this in Part 2).
. We will show this in Part 2).
So now let  and
and  be the center points of the balls bounded by
be the center points of the balls bounded by 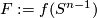 and
and 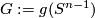 . Let
. Let 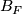 and
and 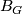 be balls bounded by
be balls bounded by  and
and  respectively. Since
respectively. Since  and
and  are locally flat, they have collar neighborhoods. Then by extending
are locally flat, they have collar neighborhoods. Then by extending 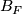 and
and 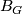 along these collars, we find open balls
along these collars, we find open balls 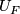 and
and 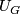 containing
containing  and
and  (respectively).
(respectively).
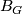 so that
so that  and
and  agree. Since
agree. Since 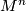 is a manifold, it is path-connected. Then there exists some continuous map
is a manifold, it is path-connected. Then there exists some continuous map ![\gamma:[0,1]\to M^n](/images/math/a/9/0/a90ee66fe3f633318d17552e55c11fd5.png) so that
so that 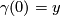 and
and 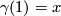 . Pick charts
. Pick charts 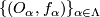 covering
covering  , where
, where 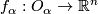 is a homeomorphism. For each
is a homeomorphism. For each ![p\in [0,1]](/images/math/3/e/8/3e861ff7f4293e5d7e6db8afd0fa5f2c.png) , Let
, Let 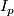 be an open (in
be an open (in ![[0,1]](/images/math/e/6/d/e6d5b5dafb82c2bf8b920a812188ac06.png) ) subinterval of
) subinterval of ![[0,1]](/images/math/e/6/d/e6d5b5dafb82c2bf8b920a812188ac06.png) containing
containing  so that
so that 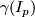 is contained in a single
is contained in a single 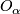 (call this
(call this 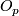 ). Then
). Then ![\{I_p\}_{p\in[0,1]}](/images/math/d/7/5/d75072ecf8bf6b02fc0fb7f2d440995b.png) is an open cover of
is an open cover of ![[0,1]](/images/math/e/6/d/e6d5b5dafb82c2bf8b920a812188ac06.png) , so from compactness there exists a finite collection
, so from compactness there exists a finite collection ![p_1<\ldots<p_k\in[0,1]](/images/math/b/2/e/b2ed49accf5e312b28ae5c9940e3fea1.png) so that
so that ![[0,1]=\cup_{i=1}^k I_{p_i}](/images/math/e/8/6/e86b7966eab58ed9c6c371092c74978a.png) . If
. If 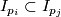 for
for 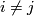 , delete
, delete 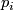 from the collection
from the collection  and relabel. Let
and relabel. Let 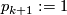 . In
. In 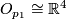 , choose a path
, choose a path 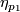 from
from  to
to 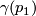 which has a tubular neighborhood
which has a tubular neighborhood 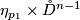 . Ambiently isotope
. Ambiently isotope 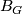 along
along 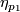 so that
so that 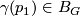 . Then ambiently isotope the interior of
. Then ambiently isotope the interior of 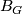 to take
to take  along
along 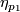 so that
so that  agrees with
agrees with 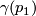 . Repeat for each
. Repeat for each 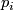 for
for 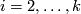 until
until  agrees with
agrees with 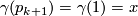 .
.
Shrink
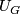 so that
so that 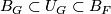 . So in
. So in 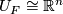 ,
,  and
and  are nested disjoint
are nested disjoint  -spheres. By the annulus conjecture,
-spheres. By the annulus conjecture,  and
and  cobound an
cobound an 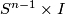 in
in 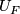 . Therefore, we may isotope
. Therefore, we may isotope  in
in 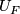 along the
along the  direction of this product until
direction of this product until  and
and  agree.
agree.
Part 2
Finally, we must show that there is a unique orientation-preserving automorphism of
 up to topological isotopy (for each
up to topological isotopy (for each  ). First we remark that if
). First we remark that if 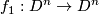 is a continuous map fixing
is a continuous map fixing 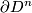 pointwise, then
pointwise, then  is isotopic rel boundary to the identity map
is isotopic rel boundary to the identity map 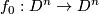 . (This is called Alexander's trick.) This can be shown constructively; consider the isotopy
. (This is called Alexander's trick.) This can be shown constructively; consider the isotopy 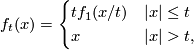 where
where 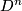 has radius
has radius  .
.
Now let
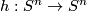 be an orientation-preserving automorphism. We will proceed by induction; as a base case consider
be an orientation-preserving automorphism. We will proceed by induction; as a base case consider 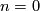 . There are two automorphisms of
. There are two automorphisms of 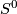 , one of which is orientation-preserving. Then the claim holds trivially.
, one of which is orientation-preserving. Then the claim holds trivially.
Now let
 be arbitrary. Let
be arbitrary. Let  be a locally flat copy of
be a locally flat copy of 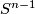 embedded in
embedded in  which splits
which splits  into two
into two  -balls. Then
-balls. Then 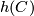 is another such copy of
is another such copy of 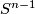 . By the argument we used above to isotope
. By the argument we used above to isotope  and
and  , we may isotope
, we may isotope  (and hence
(and hence 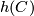 ) so that
) so that  and
and 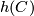 are disjoint and contained in an
are disjoint and contained in an  -ball. By the annular embedding theorem,
-ball. By the annular embedding theorem,  and
and 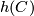 cobound an annulus, so we may isotope
cobound an annulus, so we may isotope  to fix
to fix  setwise (isotoping
setwise (isotoping 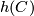 through the
through the  direction of the annulus). Call the closures of the
direction of the annulus). Call the closures of the  -ball components of
-ball components of 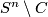
 and
and  . If
. If  reverses the orientation of
reverses the orientation of  , isotope
, isotope  to isotope one hemisphere of
to isotope one hemisphere of 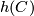 through
through  and the other through
and the other through  so that
so that  fixes
fixes  setwise and preserves the orientation of
setwise and preserves the orientation of  .
.
By induction hypothesis, isotope
 to fix
to fix  pointwise. Since
pointwise. Since  is orientation preserving,
is orientation preserving, 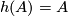 and
and 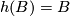 . Then by Alexander's trick,
. Then by Alexander's trick,  can be isotoped rel boundary to be the identity within
can be isotoped rel boundary to be the identity within  and
and  . Thus,
. Thus,  is isotopic to the identity.
is isotopic to the identity.