Talk:Chain duality V (Ex)

This is immediate from the definition that 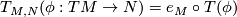$T_{M,N}(\phi:TM\to N)=e_M\circ T(\phi)$$\newcommand{\Z}{\mathbb{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\F}{\mathbb{F}} \newcommand{\bZ}{\mathbb{Z}} \newcommand{\bR}{\mathbb{R}} \newcommand{\bC}{\mathbb{C}} \newcommand{\bH}{\mathbb{H}} \newcommand{\bQ}{\mathbb{Q}} \newcommand{\bF}{\mathbb{F}} \newcommand{\bN}{\mathbb{N}} \DeclareMathOperator\id{id} % identity map \DeclareMathOperator\Sq{Sq} % Steenrod squares \DeclareMathOperator\Homeo{Homeo} % group of homeomorphisms of a topoloical space \DeclareMathOperator\Diff{Diff} % group of diffeomorphisms of a smooth manifold \DeclareMathOperator\SDiff{SDiff} % diffeomorphism under some constraint \DeclareMathOperator\Hom{Hom} % homomrphism group \DeclareMathOperator\End{End} % endomorphism group \DeclareMathOperator\Aut{Aut} % automorphism group \DeclareMathOperator\Inn{Inn} % inner automorphisms \DeclareMathOperator\Out{Out} % outer automorphism group \DeclareMathOperator\vol{vol} % volume \newcommand{\GL}{\text{GL}} % general linear group \newcommand{\SL}{\text{SL}} % special linear group \newcommand{\SO}{\text{SO}} % special orthogonal group \newcommand{\O}{\text{O}} % orthogonal group \newcommand{\SU}{\text{SU}} % special unitary group \newcommand{\Spin}{\text{Spin}} % Spin group \newcommand{\RP}{\Rr\mathrm P} % real projective space \newcommand{\CP}{\Cc\mathrm P} % complex projective space \newcommand{\HP}{\Hh\mathrm P} % quaternionic projective space \newcommand{\Top}{\mathrm{Top}} % topological category \newcommand{\PL}{\mathrm{PL}} % piecewise linear category \newcommand{\Cat}{\mathrm{Cat}} % any category \newcommand{\KS}{\text{KS}} % Kirby-Siebenmann class \newcommand{\Hud}{\text{Hud}} % Hudson torus \newcommand{\Ker}{\text{Ker}} % Kernel \newcommand{\underbar}{\underline} %Classifying Spaces for Families of Subgroups \newcommand{\textup}{\text} \newcommand{\sp}{^}T_{M,N}(\phi:TM\to N)=e_M\circ T(\phi)$.

Somewhat more elaborate, so that we really can see what's going on:

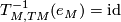We turn the question around and show that $T_{M,TM}^{-1}(e_M)=\text{id}$$T_{M,TM}^{-1}(e_M)=\text{id}$. We will suppress all decorations 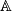$\Aa$$\Aa$ occuring in tensor products and Hom-sets and look at a sequence of maps

$\displaystyle TM\otimes M = \text{Hom}(T^2M,M) \to T^2M\otimes TM = \text{Hom}(T^3M,TM)\to M\otimes TM = \text{Hom}(TM,TM),$ $$\displaystyle TM\otimes M = \text{Hom}(T^2M,M) \to T^2M\otimes TM = \text{Hom}(T^3M,TM)\to M\otimes TM = \text{Hom}(TM,TM),$$

given by

$\displaystyle \phi\mapsto T(\phi) \mapsto (e_{T(M)}\circ T)(\phi).$ $$\displaystyle \phi\mapsto T(\phi) \mapsto (e_{T(M)}\circ T)(\phi).$$

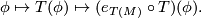
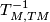This sequence of maps is precisely the previously mentioned $T_{M,TM}^{-1}$$T_{M,TM}^{-1}$. (which has hopefully been treated in the solution to exercise 10 on L-groups) Applying this map to 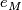$e_M$$e_M$, we get 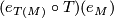$(e_{T(M)}\circ T)(e_M)$$(e_{T(M)}\circ T)(e_M)$, which is equal to the identity map, as part of its very definition.