Talk:Chain duality II (Ex)
[edit] Solution
By definition 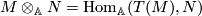 , where
, where
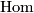 is the total complex of the Hom complex. We claim that for
is the total complex of the Hom complex. We claim that for 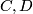 applying
applying  gives a natural map
gives a natural map 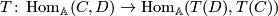 of chain complexes. We will leave
the subscript
of chain complexes. We will leave
the subscript 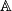 understood in the following. On double complexes
understood in the following. On double complexes
 induces
induces 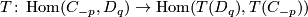 on groups and the contravariance of
on groups and the contravariance of  assures that this is still a double
complex with grading
assures that this is still a double
complex with grading 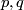 as well as the naturality of that map. It remains
to indentify
as well as the naturality of that map. It remains
to indentify 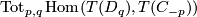 with
with
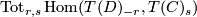 . But this holds as the
complexes are finite, so we can pull all sums out of the
. But this holds as the
complexes are finite, so we can pull all sums out of the  before any
totalization and get the same quadruple complexes. Then note that it does not
matter in which order one takes totalization.
before any
totalization and get the same quadruple complexes. Then note that it does not
matter in which order one takes totalization.
Consider the diagram
![\displaystyle \xymatrix{ \Hom(TM,N) \ar[d]_{T} & \\ \Hom(TN, T^2 M) \ar[r]^T \ar[d]_{(e_M)_*} & \Hom(T^3 M , T^2 N) \ar[d]_{(T e_M)^*} \\ \Hom(TN, M) \ar[r]^-T & \Hom(TM, T^2N) \ar[r]^{(e_N)_*} & \Hom(TM, N) }](/images/math/6/d/a/6da1904f93e6d751bd949808e79c912c.png)
It commutes because of the naturality of  . The vertical left composition
induces the map
. The vertical left composition
induces the map 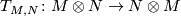 , the lower
horizontal composition the map
, the lower
horizontal composition the map 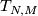 . We show the composition is the
identity. An element in
. We show the composition is the
identity. An element in 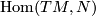 is represented by a map
is represented by a map  of chain
complexes. It gets mapped to
of chain
complexes. It gets mapped to 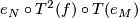 . As
. As
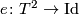 is a natural transformation
is a natural transformation 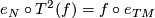 by the chain duality condition. But
by the chain duality condition. But 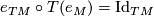 , so
, so  gets mapped to
gets mapped to  .
.