Talk:Borel conjecture in dimensions 1 and 2 (Ex)
Let us do the case of dimension  first. Here it follows from the classification that every connected closed
first. Here it follows from the classification that every connected closed  -manifold is homeomorphic to a circle
-manifold is homeomorphic to a circle  . Moreover we know that up to homotopy every self map of
. Moreover we know that up to homotopy every self map of  is of the from
is of the from 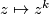 for some
for some 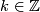 . Moreover homotopy equivalences have to fulfill
. Moreover homotopy equivalences have to fulfill 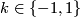 and those maps are homeomorphisms, so every homotopy equivalence is homotopic to a homeomorphism.
and those maps are homeomorphisms, so every homotopy equivalence is homotopic to a homeomorphism.
For the case of dimension  , first we note that by handle body decomposition it follows that two orientable surfaces are homotopy equivalent if and only if they are homeomorphic. For any space
, first we note that by handle body decomposition it follows that two orientable surfaces are homotopy equivalent if and only if they are homeomorphic. For any space  let us denote by
let us denote by 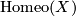 the space of homeomorphisms of
the space of homeomorphisms of  and by
and by 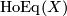 the space of homotopy equivalences of
the space of homotopy equivalences of  , each equipped with the compact open topology. We now claim that for
, each equipped with the compact open topology. We now claim that for  an orientable surface, the natural inclusion
an orientable surface, the natural inclusion
![\displaystyle \xymatrix{\mathrm{Homeo}(M) \ar[r] & \mathrm{HoEq}(M)}](/images/math/c/6/1/c619970c1fedc54a9c0127f125350e87.png)
induces a surjection on path components which follows from a theorem that this is even a bijection on path components.