Orientation of manifolds in generalized cohomology theories
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 15:36, 13 March 2014 and the changes since publication. |
|
The user responsible for this page is Yuli Rudyak. No other user may edit this page at present. |
Contents |
1 Preliminaries
One of classical definitions of orientability of a closed connected manifold  is the existence of the fundamental class
is the existence of the fundamental class ![[M]\in H_n(M)](/images/math/7/5/3/753a7f8d85351048ad0e89da15ce68f2.png) . It is clear that this definition is very suitable to generalize it to generalize (co)homology theories, and this generalization turns out to be highly productive and fruitful.
. It is clear that this definition is very suitable to generalize it to generalize (co)homology theories, and this generalization turns out to be highly productive and fruitful.
For the definition of spectra, ring spectra, etc, see [Rudyak2008].
For definitions of generalized (co)homology and their relation to spectra see [Rudyak2008].
The sign 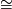 denotes an isomorphism of groups or homeomorphism of spaces.
denotes an isomorphism of groups or homeomorphism of spaces.
I reserve the term ``classical orientation`` for orientation in ordinary (co)homology, see e.g. [Kreck2013].
We denote the  th Stiefel-Whitney class by
th Stiefel-Whitney class by 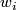 .
.
2 Basic definition
Let  be a topological
be a topological  -dimensional manifold, possibly with boundary. Consider a point
-dimensional manifold, possibly with boundary. Consider a point 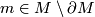 and an open disk neighborhood
and an open disk neighborhood  of
of  . Let
. Let 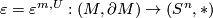 be the map that collapses the complement of
be the map that collapses the complement of  .
.
Let  be a commutative ring spectrum, and let
be a commutative ring spectrum, and let 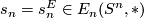 be the image of
be the image of 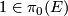 under the isomorphism
under the isomorphism
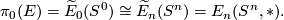
Definition 2.1. Let  be a compact topological
be a compact topological  -dimensional manifold (not necessarily connected). An element
-dimensional manifold (not necessarily connected). An element ![[M,\partial M]=[M, \partial M]_E\in E_n(M, \partial M)](/images/math/7/9/d/79d5640e6a19d1c2494ccd8a7ef0fd15.png) is called an orientation of
is called an orientation of  with respect to
with respect to  , or, briefly, an
, or, briefly, an  -orientation of
-orientation of  , if
, if ![\varepsilon_*^{m,U}[M, \partial M]=\pm s_n\in E_n(S^n,*)](/images/math/0/3/2/0325bae9311463bc08bf5ee90d3636e9.png) for every
for every  and every disk neighborhood
and every disk neighborhood  of
of  .
.
Note that a non-connected  is
is  -orientable iff all its components are.
-orientable iff all its components are.
A manifold with a fixed  -orientation is called
-orientation is called  -oriented, and a manifold which admits an
-oriented, and a manifold which admits an  -orientation is called
-orientation is called  -orientable. So, an
-orientable. So, an  -oriented manifold is in fact a pair
-oriented manifold is in fact a pair ![(M, [M]_E)](/images/math/d/2/2/d227edc2e4b030056296788630514a57.png) .
.
It follows from the classical orientability that a classically oriented manifold is 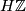 -orientable, see [Kreck2013]. Conversely, if a connected manifold is
-orientable, see [Kreck2013]. Conversely, if a connected manifold is 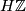 -orientable then
-orientable then 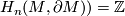 (indeed, we know that either
(indeed, we know that either 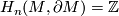 or
or 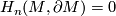 , but the second case is impossible because
, but the second case is impossible because 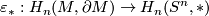 must be surjective). Hence, a connected manifold
must be surjective). Hence, a connected manifold  is
is 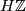 -orientable iff
-orientable iff 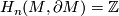 , i.e., iff
, i.e., iff  is classically orientable. Thus, for arbitrary (not necessarily connected)
is classically orientable. Thus, for arbitrary (not necessarily connected)  is
is 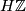 -orientable iff
-orientable iff  is classically orientable
is classically orientable
Note that 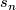 is a canonical
is a canonical  -orientation of the sphere
-orientation of the sphere  .
.
The following proposition holds because, for every two pairs 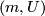 and
and 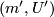 with
with  connected, the maps
connected, the maps 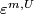 and
and 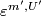 are homotopic.
are homotopic.
Proposition 2.2. Let  be a connected manifold, and let
be a connected manifold, and let 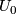 be an open disk neighborhood of a point
be an open disk neighborhood of a point 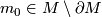 . If an element
. If an element ![[M, \partial M] \in E_n(M,\partial M)](/images/math/f/7/5/f757aeefa2ff6634041da2b9827dd728.png) is such that
is such that ![\varepsilon_*^{m_0,U_0}[M, \partial M]=\pm s_n](/images/math/9/a/7/9a782742dbc0996bacf26ddbd4b08a8d.png) , then
, then ![[M, \partial M]](/images/math/7/6/9/7695ea336d41096c1ea3c46e7bcb74b8.png) is an
is an  -orientation of
-orientation of  .
.
For the proof, see [Rudyak2008, Proposition V.2.2].
3 Number of orientations
Let  be a connected manifold. Let
be a connected manifold. Let  be and
be and  -orientation of
-orientation of  with
with 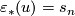 . Consider another
. Consider another  -orientation
-orientation 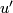 with
with 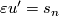 . Then
. Then 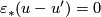 , and so
, and so 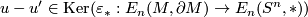 . Conversely, if
. Conversely, if 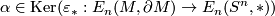 and
and  is an
is an  -orientation of
-orientation of  then
then  is an
is an  -orientation of
-orientation of  because
because 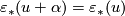 .
.
Furthermore, if  is an
is an  -orientation of
-orientation of  with
with 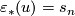 then
then 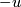 is an
is an  -orientation of
-orientation of  with
with 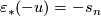 ,
,
Thus, if  is a connected
is a connected  -oriented manifold, then there is a bijection between the set of all
-oriented manifold, then there is a bijection between the set of all  -orientations of
-orientations of  and the set
and the set
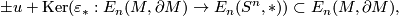
where  is any
is any  -orientation of
-orientation of  .
.
4 Relation to normal and tangent bundles
Classical orientability of a smooth manifold  is equivalent to the existence of a Thom class of the tangent (or normal) bundle of
is equivalent to the existence of a Thom class of the tangent (or normal) bundle of  , see [Kreck2013, Theorem 7.1]. The similar claim holds for generalized (co)homology.
, see [Kreck2013, Theorem 7.1]. The similar claim holds for generalized (co)homology.
Given a vector  -dimensional bundle
-dimensional bundle  over a compact space
over a compact space  , consider the Thom space
, consider the Thom space 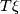 , the one-point compactification of the total space of
, the one-point compactification of the total space of  . Then for every
. Then for every 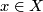 the inclusion of fiber
the inclusion of fiber 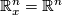 to the total space of
to the total space of  yields an inclusion
yields an inclusion 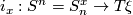 , where
, where 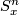 is the one-point compactification of
is the one-point compactification of 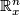 . Now, given a ring spectrum
. Now, given a ring spectrum  , note the canonical isomorphism
, note the canonical isomorphism 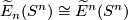 and denote by
and denote by 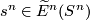 the image of
the image of 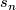 under this isomorphism.
under this isomorphism.
Definition 4.1. A Thom-Dold class of  with respect to
with respect to  (on a
(on a  -orientation of
-orientation of  ) is a class
) is a class 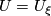 such that
such that 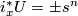 for all
for all 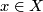 .
.
Theorem 4.2. A  smooth
smooth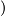 manifold
manifold  is
is  -orientable if and only if the tangent
-orientable if and only if the tangent  or normal
or normal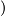 bundle of
bundle of  is
is  -orientable. Moreover,
-orientable. Moreover,  -orientations of
-orientations of  are in a bijective correspondence with
are in a bijective correspondence with  -orientations of
-orientations of  stable
stable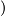 normal bundle of
normal bundle of  .
.
For the proof, see [Rudyak2008, Theorem V.2.4 and Corollary V.2.6].
Furthermore, Theorem 4.2 holds for topological manifolds as well, if we are careful with the concept of Thom spaces and their normal bundles for topological manifolds, see [Rudyak2008, Definitions IV.5.1 and IV.7.12]. To apply the theory to microbundles, use [Rudyak2008, Theorem IV.7.7].
5 Products
Here we show that the product 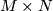 of two
of two  -oriented manifolds
-oriented manifolds 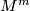 and
and 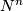 admits a canonical
admits a canonical  -orientation. For sake of simplicity, assume
-orientation. For sake of simplicity, assume  and
and  to be closed. Consider two collapsing maps
to be closed. Consider two collapsing maps 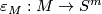 and
and 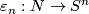 and form the map
and form the map
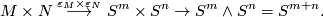
It is easy to see that this composition is (homotopic to) 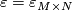 .
.
Now, let ![[M]](/images/math/f/a/0/fa08c3d5d2f54260952acc8a646b5025.png) and
and ![[N]](/images/math/3/5/8/3581986b0e7b591acd8d60e6ee096f5d.png) be
be  -orientations of
-orientations of  and
and  , respectively. Consider the commutative diagram
, respectively. Consider the commutative diagram
![\displaystyle \xymatrix{ E_m(M)\otimes E_n(N) \ar[d] \ar[r]^{\mu} & E_{m+n}(M\times N) \ar[r]^{\varepsilon_*} \ar[d]^{(\varepsilon_M)_*\otimes (\varepsilon_N)_*} & E_{m+n}(S^{m+n}) \ar[d]^{=} \\ E_m(S^m)\otimes E_n(S^n) \ar[r]^{\mu'} & E_{m+n}(S^m\times S^n) \ar[r] & E_{m+n}(S^{m+n}) }](/images/math/f/3/a/f3a1c1ab7b894025127eabe5abcd257a.png)
where 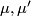 are given by the ring structure on
are given by the ring structure on  . Because of the commutativity of the above diagram, we see that
. Because of the commutativity of the above diagram, we see that ![\varepsilon_*(\mu([M]\otimes [N]))=\pm s_{m+n}](/images/math/5/8/4/5844cd9faf6ffadb274afb35a79f18c8.png) . Thus
. Thus ![[M]\otimes [N]](/images/math/e/4/b/e4b21c1da18136c5620806f2b50a4d0f.png) is an
is an  -orientation.
-orientation.
It is also worthy to note that if  and
and 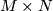 are
are  -orientable then
-orientable then  is, cf. [Rudyak2008, V.1.10(ii)].
is, cf. [Rudyak2008, V.1.10(ii)].
6 Poincaré Duality
Let  be an
be an  -module spectrum. Given a closed
-module spectrum. Given a closed  -oriented manifold
-oriented manifold ![(M, [M]_E)](/images/math/f/d/f/fdffb98222d4c6e1374536fc7cbbffd8.png) , consider the homomorphism
, consider the homomorphism
![\displaystyle \frown [M]_E: F^i(M)\to F_{n-i}(M)](/images/math/f/3/f/f3f2d32a94ffecda3bd08de12cf6ee39.png)
where 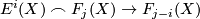 is the cap product.
is the cap product.
It turns out to be that ![\frown [M]_E](/images/math/d/5/e/d5e12b9d1b9172ca074a94721f35c47a.png) is an isomorphism. This is called Poincaré duality and is frequently denoted by
is an isomorphism. This is called Poincaré duality and is frequently denoted by 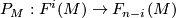 .
.
The Poincaré duality isomorphism admits the following alternative description:
![\displaystyle P=P_{[M]_E}: F^i(M) \stackrel{\varphi}\longrightarrow F^i(T\nu) \cong \widetilde F_{n-i}(M^+) =F_{n-i}(M).](/images/math/7/a/d/7adbc656efad121c0281c808e48d2c81.png)
Here 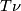 is the Thom spectrum of the stable normal bundle
is the Thom spectrum of the stable normal bundle  of
of  , and
, and 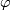 is the Thom-Dold isomorphism given by an
is the Thom-Dold isomorphism given by an  -orientation (Thom-Dold class)
-orientation (Thom-Dold class)  of
of  , which, in turn, is given by the
, which, in turn, is given by the  -orientation
-orientation ![[M]_E](/images/math/5/b/7/5b7482ce4e61e514c027215f873c10da.png) of
of  according to Theorem 4.2.
according to Theorem 4.2.
For the proofs of the statements in this section, see [Rudyak2008, Theorem 2.9].
7 Transfer
Definition 7.1. Let  be a module spectrum over a ring spectrum
be a module spectrum over a ring spectrum  . Let
. Let 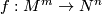 be a map of closed manifolds.
be a map of closed manifolds.
Suppose that both 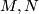 are
are  -oriented, and let
-oriented, and let 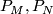 be the Poincaré duality isomorphisms, respectively. We define the transfers (other names: Umkehrs, Gysin homomorphisms)
be the Poincaré duality isomorphisms, respectively. We define the transfers (other names: Umkehrs, Gysin homomorphisms)

to be the compositions
![\displaystyle f^!: F^i(M) \cong F_{m-i}(M) \stackrel{f_*}{\longrightarrow} F_{m-i}(N) \cong F^{n-m+i}(M),\ f^!=P_{[N]}^{-1}f_*P_{[M]}, \\ f_!: F_i(N) \cong F^{n-i}(N) \stackrel{f^*}{\longrightarrow} F^{n-i}(M) \cong F_{m-n+i}(N),\ f_!=P_{[M]}f^*P_{[N]}^{-1}.](/images/math/c/4/d/c4dc3d7b23c35585797523ad6c83cdf1.png)
The reader can find many good properties of transfers in Dold [Dold1972], Dyer [Dyer1969], Rudyak [Rudyak2008].
If 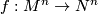 is a map of closed
is a map of closed 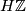 -oriented manifolds then
-oriented manifolds then
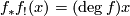
for every 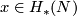 . In particular, if
. In particular, if 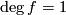 then
then 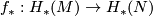 is epic. Similarly,
is epic. Similarly, 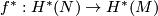 is a monomorphism if
is a monomorphism if 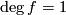 . Theorem 7.2 below generalizes this fact.
. Theorem 7.2 below generalizes this fact.
Theorem 7.2 [Rudyak2008, Lemma V.2.12 and Theorem V.2.14].
Let  be a ring spectrum. Let
be a ring spectrum. Let 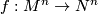 be a map of degree
be a map of degree 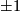 of closed
of closed 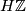 -orientable manifolds. If
-orientable manifolds. If ![[M]](/images/math/f/a/0/fa08c3d5d2f54260952acc8a646b5025.png) is an
is an  -orientation of
-orientation of  then
then ![f_*[M]](/images/math/4/4/c/44c57f9c3bf422a5986afa219eb1c0f0.png) is an
is an  -orientation of
-orientation of  . In particular, the manifold
. In particular, the manifold  is
is  -orientable if
-orientable if  is. Moreover, in this case
is. Moreover, in this case 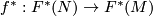 is monic and
is monic and 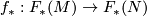 is epic for every
is epic for every  -module spectrum
-module spectrum  .
.
8 Examples
Here we list several examples.
(a) An ordinary (co)homology modulo 2. Represented by the Eilenberg-MacLane spectrum 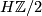 . Every manifold is
. Every manifold is 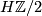 -orientable; for
-orientable; for  connected the orientation is given be modulo 2 fundamental class. see [Dold1972]. Vice versa, if a ring spectrum
connected the orientation is given be modulo 2 fundamental class. see [Dold1972]. Vice versa, if a ring spectrum  is such that every manifold is
is such that every manifold is  -orientable, then
-orientable, then  is a graded Eilenberg-MacLane spectrum and
is a graded Eilenberg-MacLane spectrum and 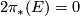 .
.
(b) An ordinary (co)homology. Represented by the Eilenberg--MacLane spectrum 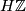 .
By Theorem 4.2 and [Rudyak2008, IV.5.8(ii)], classical orientability is just
.
By Theorem 4.2 and [Rudyak2008, IV.5.8(ii)], classical orientability is just 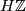 -orientability.
In particular, a smooth manifold is
-orientability.
In particular, a smooth manifold is 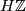 -orientable iff the structure group of its normal and/or tangent bundle can be reduced to
-orientable iff the structure group of its normal and/or tangent bundle can be reduced to 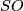 . Furthermore,
. Furthermore, 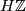 -orientability of a manifold
-orientability of a manifold  is equivalent to the equality
is equivalent to the equality 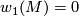 .
.
(c) 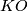 -theory. Atiyah-Bott-Shapiro [Atiyah&Bott&Shapiro1964] proved that a smooth manifold
-theory. Atiyah-Bott-Shapiro [Atiyah&Bott&Shapiro1964] proved that a smooth manifold  is
is 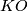 -orientable if and only if it admits a
-orientable if and only if it admits a 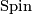 -structure. This holds, in turn, iff
-structure. This holds, in turn, iff 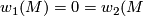 . This condition is purely homotopic and can be formulated for every topological manifold (in fact, for Poincaré spaces) in view the equality
. This condition is purely homotopic and can be formulated for every topological manifold (in fact, for Poincaré spaces) in view the equality 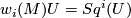 where
where  is the modulo 2 Thom class of the tangent bundle.
is the modulo 2 Thom class of the tangent bundle.
The equality 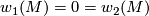 is necessary for
is necessary for 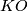 -orientability of topological manifolds, but it is not sufficient for
-orientability of topological manifolds, but it is not sufficient for 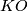 -orientability even of piecewise linear manifolds, see [Rudyak2008, Ch. VI]. One the other hand, Sullivan proved that every topological manifold is
-orientability even of piecewise linear manifolds, see [Rudyak2008, Ch. VI]. One the other hand, Sullivan proved that every topological manifold is ![KO[1/2]](/images/math/4/5/9/4598cf2e1e8fd09847861e15bf1aa1b2.png) -orientable, see Madsen-Milgram [Madsen&Milgram1979] for a good proof. Here
-orientable, see Madsen-Milgram [Madsen&Milgram1979] for a good proof. Here ![KO[1/2]](/images/math/4/5/9/4598cf2e1e8fd09847861e15bf1aa1b2.png) is the
is the ![\Z[1/2]](/images/math/7/8/e/78e1094116e3e166617d9e01262d7257.png) -localized
-localized 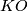 -theory.
-theory.
Note that complex manifold are  -oriented for all
-oriented for all  from (a,b,c) (but not (d, e) below).
from (a,b,c) (but not (d, e) below).
(d) Complex  -theory. The complexification
-theory. The complexification 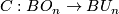 induces a ring morphism
induces a ring morphism 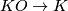 . So, every
. So, every 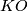 -orientable manifold is
-orientable manifold is  -orientable.
-orientable.
Atiyah-Bott-Shapiro [Atiyah&Bott&Shapiro1964] proved that a smooth manifold  is
is  -orientable iff it admits a
-orientable iff it admits a 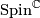 -structure. The last condition is equivalent to the purely homotopic conditions
-structure. The last condition is equivalent to the purely homotopic conditions 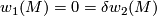 , where
, where 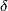 is the connecting homomorphism in the Bockstein exact sequence
is the connecting homomorphism in the Bockstein exact sequence
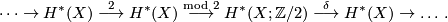
This condition is necessary for  -orientability of manifolds, but it is not sufficient for
-orientability of manifolds, but it is not sufficient for  -orientability of piecewise linearly (and hence topological) manifolds, see [Rudyak2008, Ch. VI]. On the other hand, every classically oriented topological manifold is
-orientability of piecewise linearly (and hence topological) manifolds, see [Rudyak2008, Ch. VI]. On the other hand, every classically oriented topological manifold is ![K[1/2]](/images/math/9/9/9/999aae81d8798e020a2179c030378413.png) -orientable in view of Sullivan's result mentioned in example (c).
-orientable in view of Sullivan's result mentioned in example (c).
(e) Stable (co)homotopy groups, or frames (co)bordism theory. Represented by the spectrum  . Because of Theorem 4.2, a manifold
. Because of Theorem 4.2, a manifold 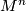 is orientable with respect to the sphere spectrum
is orientable with respect to the sphere spectrum  iff its tangent bundle
iff its tangent bundle 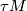 has trivial stable fiber homotopy type, i.e., iff there exists
has trivial stable fiber homotopy type, i.e., iff there exists  such that
such that 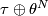 is equivalent to
is equivalent to 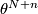 where
where 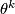 is a trivial
is a trivial  -dimensional bundle. In particular, we have the following necessary (but not sufficient) condition:
-dimensional bundle. In particular, we have the following necessary (but not sufficient) condition: 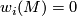 for all
for all  .
.
Note that  -orientability implies
-orientability implies 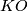 -orientability implies
-orientability implies  -orientability implies
-orientability implies 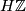 -orientability implies
-orientability implies 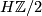 -orientability. Furthermore, any
-orientability. Furthermore, any  -orientable manifold is
-orientable manifold is  -orientable for every ring spectrum
-orientable for every ring spectrum  , cf. [Rudyak2008, I.1.6]. So, (a) and (e) appear as two extremal cases.
, cf. [Rudyak2008, I.1.6]. So, (a) and (e) appear as two extremal cases.
9 References
- [Atiyah&Bott&Shapiro1964] M. F. Atiyah, R. Bott and A. Shapiro, Clifford modules, Topology 3 (1964), suppl. 1, 3–38. MR0167985 (29 #5250) Zbl 0146.19001
- [Dold1972] A. Dold, Lectures on algebraic topology, Springer-Verlag, Berlin-Heidelberg-New York 1972. MR0415602 (54 #3685) Zbl 0234.55001
- [Dyer1969] E. Dyer, Cohomology theories, Lecture Note Series, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0268883 (42 #3780) Zbl 0182.57002
- [Kreck2013] M. Kreck, Orientation of manifolds, Bull. Man. Atl. (2013).
- [Madsen&Milgram1979] I. Madsen and R. J. Milgram, The classifying spaces for surgery and cobordism of manifolds, Princeton University Press, Princeton, N.J., 1979. MR548575 (81b:57014) Zbl 0446.57002
- [Rudyak2008] Y. B. Rudyak, On Thom spectra, orientability, and cobordism, Springer-Verlag, 1998, Corrected reprint 2008. MR1627486 (99f:55001) Zbl 0906.55001
10 External links
- The Encylopedia of Mathematics article on orientation.
- The Wikipedia page on orientability.
- The Wikipedia page on orientations of vector spaces.