Orientation of Fredholm maps between Hilbert manifolds
|
The users responsible for this page are: Matthias Kreck, Haggai Tene. No other users may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Though one can define a notion of an oriention of a manifold in the setting of Banach manifolds (namely, for Fredholm manifolds) as was done in [Elworty&Tromba1970], it seems that the more natural concept is that of an orientation of a map between such manifolds. In this note we define a notion of an orientation of a Fredholm map between Hilbert manifolds. We don't claim any originality. Related notions were given in [Morava1968], [Fitzpatrick&Pejsachowicz&Rabier1994] and [Benevieri&Furi1998] for non-linear maps between Banach spaces. The definition of an orientation is given in terms of a line bundle, the determinant line bundle. Our construction of the determinant line bundle agrees with that of [Wang2005] but he defines orientation only for index 0 Fredholm maps (since he is interested in the degree of proper Fredholm maps). We also add some useful information like orientation of a composition of two maps and product orientations.
Contents |
1 Introduction
Given a Fredholm map 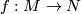 we want to construct the determinant line bundle. The rough idea is to consider the tensor product of the determinant line bundle of the kernel "bundle" of the differential of
we want to construct the determinant line bundle. The rough idea is to consider the tensor product of the determinant line bundle of the kernel "bundle" of the differential of 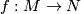 with the pullback of the determinant line bundle of the cokernel "bundle". Unless the dimension of
with the pullback of the determinant line bundle of the cokernel "bundle". Unless the dimension of 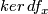 is constant, these are not bundles and thus one has to make sense of these constructions. We will do this by following Jänich's construction of an index bundle for a Fredholm map. This is similar to the construction of the determinant line bundle in [Quillen1985].
is constant, these are not bundles and thus one has to make sense of these constructions. We will do this by following Jänich's construction of an index bundle for a Fredholm map. This is similar to the construction of the determinant line bundle in [Quillen1985].
2 Definition
Let 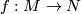 be a Fredholm map. We equip
be a Fredholm map. We equip  and
and  with Riemannian metrics. For each
with Riemannian metrics. For each 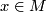 we will construct an open neighborhood
we will construct an open neighborhood  and a line bundle
and a line bundle  over
over  depending on a choice. For different choices one has explicit isomorphisms which are compatible with restrictions to open subsets of
depending on a choice. For different choices one has explicit isomorphisms which are compatible with restrictions to open subsets of  . These isomorphisms depend only on the metric and the differential of
. These isomorphisms depend only on the metric and the differential of  and so one can glue these bundles together to obtain the desired global line bundle. Since the space of metrics is convex the resulting bundle is also independent of the metric.
and so one can glue these bundles together to obtain the desired global line bundle. Since the space of metrics is convex the resulting bundle is also independent of the metric.
To find such an open neighborhood  of
of  and the desired line bundle over
and the desired line bundle over  we note that the arguments in [Jänich1965, Lemma 3] (he constructs for compact spaces a global object, but the first step is the local object, and that's all we need) implies that for each
we note that the arguments in [Jänich1965, Lemma 3] (he constructs for compact spaces a global object, but the first step is the local object, and that's all we need) implies that for each  in
in  there is an open neighborhood
there is an open neighborhood  and a finite dimensional subbundle
and a finite dimensional subbundle  of
of 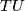 such that
such that 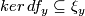 for all
for all 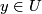 . Let
. Let 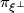 be the orthogonal projection to the orthogonal complement of
be the orthogonal projection to the orthogonal complement of  in
in 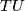 . Then
. Then 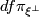 is a Fredholm bundle map and its kernel is the subbundle
is a Fredholm bundle map and its kernel is the subbundle  [Jänich1965, p. 138]. Thus the cokernel bundle with fibre over
[Jänich1965, p. 138]. Thus the cokernel bundle with fibre over 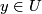 the cokernel of
the cokernel of 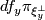 is defined and denoted by
is defined and denoted by 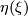 . To avoid signs, when
we define the product orientation and interchange the factors we always assume that
. To avoid signs, when
we define the product orientation and interchange the factors we always assume that 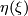 is even dimensional, which can be achieved by stabilizing
is even dimensional, which can be achieved by stabilizing  and by this
and by this 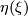 , if
necessary. We define a line bundle over
, if
necessary. We define a line bundle over  by
by 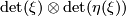 , where
, where 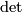 denotes the determinant line bundle, and denote it by
denotes the determinant line bundle, and denote it by 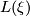 . If
. If 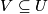 is open then
is open then 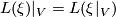 .
.
If 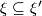 is a subbundle, the differential of
is a subbundle, the differential of  and the Riemannian metric can be used to construct explicit isomorphisms
and the Riemannian metric can be used to construct explicit isomorphisms 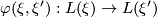 . For this we note that - using the Riemannian metric - we have an embedding of
. For this we note that - using the Riemannian metric - we have an embedding of 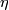 into
into 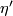 and that Jänich shows ([Jänich1965], p. 138) that the differential induces an isomorphism
and that Jänich shows ([Jänich1965], p. 138) that the differential induces an isomorphism 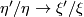 . Since for all
. Since for all  and
and 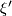 there is a common finite dimensional subbundle of
there is a common finite dimensional subbundle of 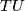 containing both one obtains isomorphisms
containing both one obtains isomorphisms 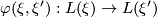 in general.
in general.
Now we glue all these line bundles over such open subsets  in
in  together using the isomorphisms
together using the isomorphisms 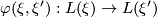 and the fact that everything is compatible with restrictions and the construction of
and the fact that everything is compatible with restrictions and the construction of 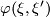 based on the differential (and the global Riemannian metric) fulfills the cocycle conditions, since they are induced by differentials. This is our determinant line bundle
based on the differential (and the global Riemannian metric) fulfills the cocycle conditions, since they are induced by differentials. This is our determinant line bundle 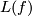 over
over  .
.
Definition 2.1.
An orientation of a Fredholm map 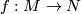 is an orientation of
is an orientation of 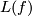 .
If we replace the orientation on
.
If we replace the orientation on 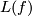 by the opposite orientation we call the corresponding Fredholm map
by the opposite orientation we call the corresponding Fredholm map 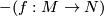
Lemma 2.2.
If 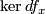 has constant dimension then
has constant dimension then
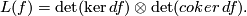
Proof.
Take  to be
to be 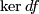 globally.
globally.

3 Orientation of compositions
Given two Fredholm maps 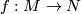 and
and 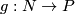 , it follows from the proof of [Jänich1965, Lemma 6] that there is an explicit isomorphism
, it follows from the proof of [Jänich1965, Lemma 6] that there is an explicit isomorphism
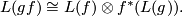
Thus if both maps are oriented one obtains an induced orientation of the composition by using the isomorphism above to orient 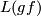 .
.
4 Product orientation
Given two oriented Fredholm maps
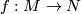 and
and 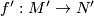 , we would like to orient the product map
, we would like to orient the product map 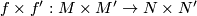 . For this we consider the local construction of
. For this we consider the local construction of
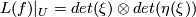 and similarly
and similarly 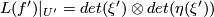 and obtain:
and obtain: 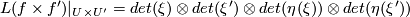 .
By interchanging the factors in the middle we identify this with
.
By interchanging the factors in the middle we identify this with 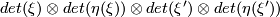 . Recall that we always assume the
. Recall that we always assume the 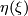 is even
dimensional. Then we take the product orientation on
is even
dimensional. Then we take the product orientation on 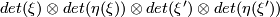 and equip
and equip 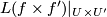 with the induced orientation given by the isomorphism
interchanging the middle factors.
with the induced orientation given by the isomorphism
interchanging the middle factors.
5 Orientation of the cylinder and of the boundary of a Fredholm map
A useful thing for coboridsm is to orient the cylinder 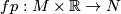 , where
, where  is the projection to
is the projection to  . As explained before, this is an orientation of
. As explained before, this is an orientation of 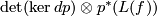 , and since
, and since 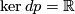 , the trivial bundle, it is equivalent to an orientation of
, the trivial bundle, it is equivalent to an orientation of 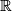 and of
and of  . If we change the orientation on
. If we change the orientation on 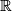 we obtain the opposite orientation. Using this and a collar we orient the boundary of a Fredholm map.
we obtain the opposite orientation. Using this and a collar we orient the boundary of a Fredholm map.
6 Orientation of maps in finite dimensions
This construction also works for maps between finite dimensional manifolds. In this case we can choose globally  as
as  , then we get
, then we get
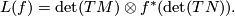
If we denote by  the infinite dimensional separable Hilbert space, then for the product map
the infinite dimensional separable Hilbert space, then for the product map 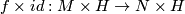 we have
we have
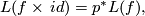
where  is the projection from
is the projection from 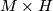 to
to  , since in this case we note that we can choose
, since in this case we note that we can choose  to be
to be 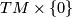 .
.
Remark 6.1. The above implies that a map between oriented finite dimensional manifolds has a natural orientation in this sense.
7 References
- [Benevieri&Furi1998] T. P. Benevieri and M. Furi, A simple notion of orientability for Fredholm maps of index zero between Banach manifolds and degree theory, Ann. Sci. Math. Québec 22 (1998), 131-148. MR1677235 (2000a:58024) Zbl 1058.58502
- [Elworty&Tromba1970] K. D. Elworthy and A. J. Tromba, Differential structures and Fredholm maps in Banach manifolds, Global analysis (Berkeley, 1968), Proc. Sympos. Pure Math., 15, pp. 45--94, Amer. Math. Soc., Providence, RI, 1970. MR0264708 (41 #9299) Zbl 0206.52504
- [Fitzpatrick&Pejsachowicz&Rabier1994] P. M. Fitzpatrick, J. Pejsachowicz, and P. J. Rabier, Orientability of Fredholm families and topological degree for orientable non-linear Fredholm mappings, J. Funct. Anal. 124 (1994), 1--39. MR1284601 Zbl 0802.47056
- [Jänich1965] T. K. Jänich, Vektorraumbündel und der Raum der Fredholm-Operatoren, Math. Ann. 161, 1965 129–142. MR0190946 (32 #8356) Zbl 0148.12401
- [Morava1968] J. J. Morava, Algebraic topology of Fredholm maps, Thesis (Ph.D.)–Rice University. 1968. MR2617315
- [Quillen1985] D. Quillen, Determinants of Cauchy–Riemann operators on Riemann surfaces, Funct. Anal. Appl., 19 (1) (1985), pp. 31–34. MR0783704 Zbl 0603.32016
- [Wang2005] S. Wang, On orientability and degree of Fredholm maps, Michigan Math. J. 53 (2005), no. 2, 419–428. MR2152708 Zbl 1093.58003