Geometric 3-manifolds
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
Let a group  act on a manifold
act on a manifold  by homeomorphisms.
by homeomorphisms.
A 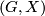 -manifold is a manifold
-manifold is a manifold  with a
with a 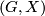 -atlas, that is, a collection
-atlas, that is, a collection 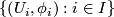 of homeomorphisms
of homeomorphisms
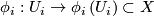
onto open subsets of  such that all coordinate changes
such that all coordinate changes
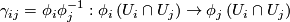
are restrictions of elements of  .
.
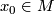 and a chart
and a chart 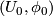 with
with 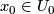 . Let
. Let 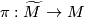 be the universal covering. These data determine the developing map
be the universal covering. These data determine the developing map 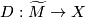
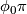 along each path, in a neighborhood of the path's endpoint.
along each path, in a neighborhood of the path's endpoint.
If we change the initial data 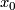 and
and 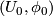 , the developing map
, the developing map 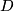 changes by composition with an element of
changes by composition with an element of  .
.
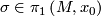 , analytic continuation along a loop representing
, analytic continuation along a loop representing 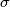 gives a chart
gives a chart 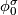 that is comparable to
that is comparable to 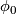 , since they are both defined at
, since they are both defined at 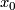 . Let
. Let 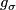 be the element of
be the element of  such that
such that 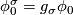 . The map
. The map 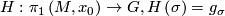
is a group homomorphism and is called the holonomy of  .
.
If we change the initial data 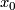 and
and 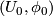 , the holonomy homomorphisms
, the holonomy homomorphisms  changes by conjugation with an element of
changes by conjugation with an element of  .
.
A 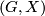 -manifold is complete if the developing map
-manifold is complete if the developing map 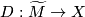 is surjective.
is surjective.
[Thurston1997] Section 3.4
Definition 1.1.
A model geometry 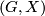 is a smooth manifold
is a smooth manifold  together with a Lie group of diffeomorphisms of
together with a Lie group of diffeomorphisms of  , such that:
, such that:
a)  is connected and simply connected;
is connected and simply connected;
b)  acts transitively on
acts transitively on  , with compact point stabilizers;
, with compact point stabilizers;
c)  is not contained in any larger group of diffeomorphisms of
is not contained in any larger group of diffeomorphisms of  with compact point stabilizers;
with compact point stabilizers;
d) there exists at least one compact 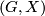 -manifold.
-manifold.
[Thurston1997] Definition 3.8.1
A 3-manifold is said to be a geometric manifold if it is a 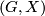 -manifold for a 3-dimensional model geometry
-manifold for a 3-dimensional model geometry 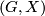 .
.
[edit] 2 Construction and examples
Theorem 2.1.There are eight 3-dimensional model geometries:
- the round sphere: 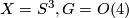
- Euclidean space: 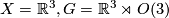
- hyperbolic space: 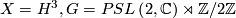
- 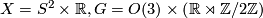
- 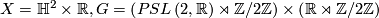
- the universal covering of the unit tangent bundle of the hyperbolic plane: 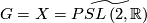
- the Heisenberg group: 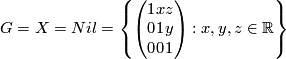
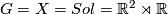 with conjugation
with conjugation 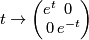 .
.[Thurston1997] Section 3.8
Outline of Proof:
Let  be the connected component of the identity of
be the connected component of the identity of  , and let
, and let 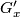 be the stabiliser of
be the stabiliser of 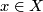 .
.
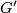 acts transitively and
acts transitively and 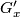 is a closed, connected subgroup of
is a closed, connected subgroup of 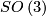 .
.
Case 1: 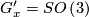 . Then
. Then  has constant sectional curvature. The Cartan Theorem implies that (up to rescaling)
has constant sectional curvature. The Cartan Theorem implies that (up to rescaling)  is isometric to one of
is isometric to one of 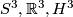 .
.
Case 2: 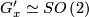 . Let
. Let  be the
be the 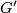 -invariant vector field such that, for each
-invariant vector field such that, for each 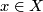 , the direction of
, the direction of 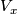 is the rotation axis of
is the rotation axis of 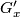 .
.  descends to a vector field on compact
descends to a vector field on compact 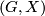 -manifolds, therefore the flow of
-manifolds, therefore the flow of  must preserve volume. In our setting this implies that the flow of
must preserve volume. In our setting this implies that the flow of  acts by isometries. Hence the flowlines define a 1-dimensional foliation
acts by isometries. Hence the flowlines define a 1-dimensional foliation 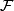 with embedded leaves. The quotient
with embedded leaves. The quotient 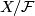 is a 2-dimensional manifold, which inherits a Riemannian metric such that
is a 2-dimensional manifold, which inherits a Riemannian metric such that 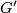 acts transitively by isometries. Thus
acts transitively by isometries. Thus 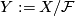 has constant curvature and is (up to rescaling) isometric to one of
has constant curvature and is (up to rescaling) isometric to one of 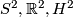 .
.  is a pricipal bundle over
is a pricipal bundle over  with fiber
with fiber 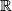 or
or  ,
The plane field
,
The plane field  orthogonal to
orthogonal to  has constant curvature, hence it is either a foliation or a contact structure.
has constant curvature, hence it is either a foliation or a contact structure.
Case 2a:  is a foliation. Thus
is a foliation. Thus  is a flat bundle over
is a flat bundle over  .
.  is one of
is one of 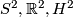 , hence
, hence 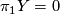 , which implies that
, which implies that 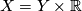 .
.
Case 2b:  is a contact structure.
For
is a contact structure.
For 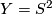 one would obtain for
one would obtain for  the group of isometries of
the group of isometries of  that preserve the Hopf fibration. This is not a maximal group with compact stabilizers, thus there is no model geometry in this case.
For
that preserve the Hopf fibration. This is not a maximal group with compact stabilizers, thus there is no model geometry in this case.
For 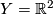 one obtains
one obtains 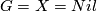 . Namely,
. Namely,  is the subgroup of the group of automorphisms of the standard contact structure
is the subgroup of the group of automorphisms of the standard contact structure 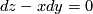 on
on 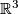 consisting of those automorphisms which are lifts of isometries of the x-y-plane.
For
consisting of those automorphisms which are lifts of isometries of the x-y-plane.
For 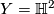 one obtains
one obtains 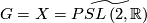 .
.
Case 3: 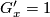 . Then
. Then 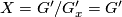 is a Lie group. The only 3-dimensional unimodular Lie group which is not subsumed by one of the previous geometries is
is a Lie group. The only 3-dimensional unimodular Lie group which is not subsumed by one of the previous geometries is 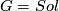 .
.
[edit] 3 Invariants
...
[edit] 4 Classification/Characterization
A closed 3-manifold is called:
- irreducible, if every embedded 2-sphere bounds an embedded 3-ball,
- geometrically atoroidal, if there is no embedded incompressible torus,
- homotopically atoroidal, if there is no immersed incompressible torus.
Theorem 4.1 (Geometrization).
Let  be a closed, orientable, irreducible, geometrically atoroidal 3-manifold.
be a closed, orientable, irreducible, geometrically atoroidal 3-manifold.
a) If  is homotopically atoroidal, then it admits an
is homotopically atoroidal, then it admits an 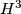 -geometry.
-geometry.
b) If  is not homotopically atoroidal, then it admits (at least) one of the seven non-
is not homotopically atoroidal, then it admits (at least) one of the seven non-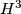 -geometries.
-geometries.
Example 4.2 (Geometrization of mapping tori).
Let 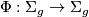 be an orientation-preserving homeomorphism of the surface of genus
be an orientation-preserving homeomorphism of the surface of genus  .
.
a) If 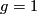 , then the mapping torus
, then the mapping torus 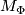 satisfies the following:
satisfies the following:
1. If 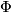 is periodic, then
is periodic, then 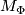 admits an
admits an 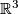 geometry.
geometry.
2. If 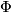 is reducible, then
is reducible, then 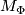 contains an embedded incompressible torus.
contains an embedded incompressible torus.
3. If 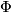 is Anosov, then
is Anosov, then 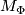 admits a
admits a 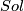 geometry.
geometry.
b) If 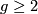 , then the mapping torus
, then the mapping torus 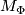 satisfies the following:
satisfies the following:
1. If 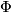 is periodic, then
is periodic, then 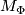 admits an
admits an 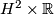 -geometry.
-geometry.
2. If 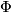 is reducible, then
is reducible, then 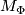 contains an embedded incompressible torus.
contains an embedded incompressible torus.
3. If 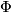 is pseudo-Anosov, then
is pseudo-Anosov, then 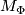 admits an
admits an 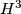 -geometry.
-geometry.
As the example suggests, the most abundant case ist that of Hyperbolic 3-manifolds.
[edit] 5 Further discussion
...
[edit] 6 References
- [Thurston1997] W. P. Thurston, Three-dimensional geometry and topology. Vol. 1, Princeton University Press, Princeton, NJ, 1997. MR1435975 (97m:57016) Zbl 0873.57001