Fundamental class
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 15:25, 6 March 2014 and the class&diff=cur&oldid=11505 changes since publication. |
|
The user responsible for this page is Matthias Kreck. No other user may edit this page at present. |
Contents |
1 The integral fundamental class
For compact manifolds one can characterize the orientability by the existence of a certain homology class called the fundamental class. The background is the following theorem. Recall that
if  is an
is an  -dimensional topological manifold (possibly with boundary), then for each
-dimensional topological manifold (possibly with boundary), then for each  in the interior of
in the interior of  , one has
, one has 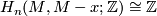 , [Greenberg&Harper1981, 22.1].
, [Greenberg&Harper1981, 22.1].
Theorem 1.1.
Let  be an
be an  -dimensional compact topological manifold (possibly with boundary).
If
-dimensional compact topological manifold (possibly with boundary).
If  is connected and orientable then for each x in the interior of
is connected and orientable then for each x in the interior of  , the map induced by the inclusion
, the map induced by the inclusion
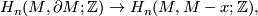
is an isomorphism. In particular, 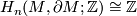 .
If
.
If  is connected and non-orientable then
is connected and non-orientable then 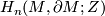 is zero.
is zero.
 is closed then this is part of [Dold1995, VIII Corollary 3.4]; see also [Greenberg&Harper1981, 22.26]. If
is closed then this is part of [Dold1995, VIII Corollary 3.4]; see also [Greenberg&Harper1981, 22.26]. If  has a boundary
has a boundary 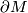 , then the inclusion
, then the inclusion 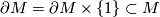 extends to an embedding
extends to an embedding 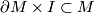 of a collar, where
of a collar, where ![I=[0,1]](/images/math/1/c/a/1ca01533a825141b051c7492a6fa6427.png) [Hatcher2002, Proposition 3.42]. Let
[Hatcher2002, Proposition 3.42]. Let Tex syntax error, so that
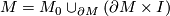 . By excision
. By excision
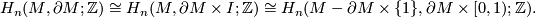
Now apply [Dold1995, VIII Corollary 3.4] to the open manifold 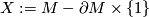 and the closed subset
and the closed subset 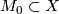 .
.

 is orientable if and only if
is orientable if and only if 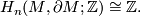
![[M,\partial M] \in H_n(M,\partial M;\mathbb Z)](/images/math/9/c/6/9c65137bf5f40d4546f27964b7a7e049.png) for
for  . The fundamental class determines by the isomorphism above a continuous choice of local orientations and in turn the fundamental class is determined by a homological orientation of
. The fundamental class determines by the isomorphism above a continuous choice of local orientations and in turn the fundamental class is determined by a homological orientation of  . In other words a connected compact manifold together with the choice of a fundamental class
. In other words a connected compact manifold together with the choice of a fundamental class ![[M,\partial M]](/images/math/f/d/e/fdeedcf7ff8b488cd51bffc2e0ad8969.png) is the same as an oriented manifold. If
is the same as an oriented manifold. If  is not connected, then
is not connected, then  is orientable if and only all components are orientable. If the components are oriented the fundamental classes of the components give the fundamental class of
is orientable if and only all components are orientable. If the components are oriented the fundamental classes of the components give the fundamental class of  under the isomorphism which decomposes the homology groups into the homology groups of the components. Thus for oriented manifolds again one has a fundamental class which corresponds to a orientation as in the connected case. The construction of the fundamental class of an oriented closed manifold is done inductively over an atlas (similarly for manifolds with boundary). Namely one has the following generalization of Theorem 1:
under the isomorphism which decomposes the homology groups into the homology groups of the components. Thus for oriented manifolds again one has a fundamental class which corresponds to a orientation as in the connected case. The construction of the fundamental class of an oriented closed manifold is done inductively over an atlas (similarly for manifolds with boundary). Namely one has the following generalization of Theorem 1:
Theorem 1.2 [Greenberg&Harper1981, 22.24] . Let  be a connected oriented
be a connected oriented  -dimensional manifold. Then for each compact subset
-dimensional manifold. Then for each compact subset  there is a class
there is a class ![[M]_K \in H_n(M, M-K)](/images/math/a/8/2/a82e287e227ee1d1fbd70a54ca5ad250.png) such that the following hold.
such that the following hold.
- If
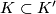 is another compact subset, then
is another compact subset, then ![[M]_K'](/images/math/f/1/6/f16c6b39e9f758614ec85ba37b44038a.png) maps to
maps to 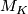 under the map induced by the inclusion.
under the map induced by the inclusion.
- For each
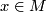 the class
the class ![[M]_x](/images/math/8/b/d/8bd566976180c686a502d2a1cbce67f1.png) is the local orientation of
is the local orientation of  .
.
- The classes
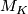 are uniquely characterized by these properties.
are uniquely characterized by these properties.
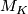 . The inductive construction is rather indirect. If one defines the homology of a space
. The inductive construction is rather indirect. If one defines the homology of a space  as the bordism classes of certain stratified spaces
as the bordism classes of certain stratified spaces  together with a continuous map to
together with a continuous map to  , e.g. stratifolds, then the the fundamental class is easy to obtain, it is a tautology. Then the fundamental class of a closed manifold is the bordism class represented by the identity map
, e.g. stratifolds, then the the fundamental class is easy to obtain, it is a tautology. Then the fundamental class of a closed manifold is the bordism class represented by the identity map 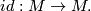
2 The Z/2-fundamental class
 -dimensional connected compact manifolds - even if they are not orientable - one has
-dimensional connected compact manifolds - even if they are not orientable - one has 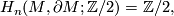
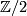 -fundamental class [Dold1995, VIII Definition 4.1]. As for the integral fundamental class (if
-fundamental class [Dold1995, VIII Definition 4.1]. As for the integral fundamental class (if  is oriented) one gets from these classes the
is oriented) one gets from these classes the 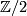 -fundamental class of a non-connected compact manifold. Also one has a generalization of Theorem 1.2 to non-compact connected manifolds, i.e. for each compact subset
-fundamental class of a non-connected compact manifold. Also one has a generalization of Theorem 1.2 to non-compact connected manifolds, i.e. for each compact subset  one has
one has 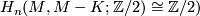 and for
and for 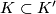 the map induced by the inclusion is an ismorphism
the map induced by the inclusion is an ismorphism 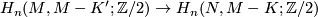 .
.
3 References
- [Dold1995] A. Dold, Lectures on algebraic topology, Springer-Verlag, 1995. MR1335915 (96c:55001) Zbl 0872.55001
- [Greenberg&Harper1981] M. J. Greenberg and J. R. Harper, Algebraic topology, Benjamin/Cummings Publishing Co. Inc. Advanced Book Program, 1981. MR643101 (83b:55001) Zbl 0498.55001
- [Hatcher2002] A. Hatcher, Algebraic topology, Cambridge University Press, 2002. MR1867354 (2002k:55001) Zbl 1044.55001
- [Kreck2010] M. Kreck, Differential algebraic topology, Graduate Studies in Mathematics, 110, American Mathematical Society, 2010. MR2641092 (2011i:55001) Zbl 05714474
4 External links
- The Encylopedia of Mathematics article on the fundamental class.
- The Wikipedia page on the fundamental class.