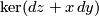Contact manifold
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 15:15, 19 November 2013 and the changes since publication. |
|
The user responsible for this page is Hansjörg Geiges. No other user may edit this page at present. |
Contents |
1 Definition
Let  be a differential manifold,
be a differential manifold,  its tangent bundle, and
its tangent bundle, and 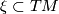 a field of hyperplanes on
a field of hyperplanes on  , that is, a smooth sub-bundle of codimension
, that is, a smooth sub-bundle of codimension  . Here the terms `differential' and `smooth' are used synonymously with
. Here the terms `differential' and `smooth' are used synonymously with 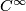 . Locally,
. Locally,  can be written as the kernel of a non-vanishing differential
can be written as the kernel of a non-vanishing differential  -form
-form  . A
. A  -form
-form  defined globally on
defined globally on  with
with 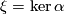 can be found if and only if
can be found if and only if  is coorientable, which is equivalent to saying that the quotient line bundle
is coorientable, which is equivalent to saying that the quotient line bundle 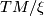 is trivial. The
is trivial. The  -form
-form  is determined by
is determined by  up to multiplication by a smooth function
up to multiplication by a smooth function 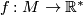 or, if the coorientation of
or, if the coorientation of  has been fixed, by a function taking positive real values only. An equation of the form
has been fixed, by a function taking positive real values only. An equation of the form 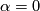 , with
, with  a non-vanishing
a non-vanishing  -form, is classically referred to as a Pfaffian equation.
-form, is classically referred to as a Pfaffian equation.
Definition 1.1.
Let  be a smooth manifold of odd dimension
be a smooth manifold of odd dimension 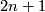 . A contact structure on
. A contact structure on  is a hyperplane field
is a hyperplane field 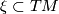 whose (locally) defining
whose (locally) defining  -form
-form  has the property that the
has the property that the 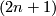 -form
-form 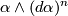 is nowhere zero, i.e. a volume form, on its domain of definition.
is nowhere zero, i.e. a volume form, on its domain of definition.
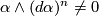 is indeed a property of
is indeed a property of  and independent of the choice of defining
and independent of the choice of defining  -form
-form  , since
, since 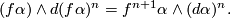
Definition 1.2.
A pair 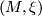 consisting of an odd-dimensional manifold
consisting of an odd-dimensional manifold  and a contact structure
and a contact structure  on
on  is called a contact manifold.
is called a contact manifold.
Definition 1.3.
A  -form as in Definition 1.1, defined globally on
-form as in Definition 1.1, defined globally on  , is called a contact form on
, is called a contact form on  .
.
Occasionally the terminology strict contact manifold is used to denote a pair 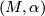 consisting of an odd-dimensional manifold and a contact form on it.
consisting of an odd-dimensional manifold and a contact form on it.
2 Examples
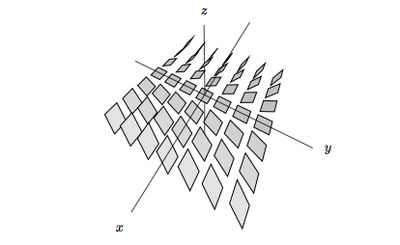
2.1 The standard contact structure on R2n+1
On 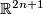 with Cartesian coordinates
with Cartesian coordinates
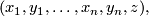
 -form
-form 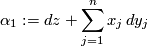
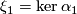 is called the standard contact structure on
is called the standard contact structure on 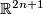 . See Figure 1 for the
. See Figure 1 for the  -dimensional case.
-dimensional case.
The theorem of Darboux states that locally any contact structure looks like the standard one, cf. [Geiges2008, Theorem 2.5.1].
Theorem 2.1 (Darboux).
Let be a contact form on the
be a contact form on the 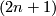 -dimensional manifold
-dimensional manifold  and
and  a point in
a point in  . Then there are coordinates
. Then there are coordinates 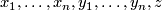 on a neighbourhood
on a neighbourhood 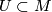 of
of  such that
such that 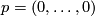 and
and 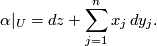
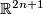 is given by the contact form
is given by the contact form 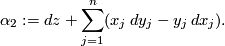
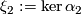 is equivalent to
is equivalent to 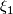 in the following sense.
in the following sense.
Definition 2.2.
Two contact manifolds 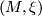 ,
, 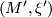 are said to be contactomorphic if there is a diffeomorphism
are said to be contactomorphic if there is a diffeomorphism 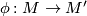 with
with 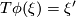 , where
, where 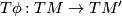 denotes the differential of
denotes the differential of  . If
. If 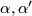 are contact forms defining the contact structures
are contact forms defining the contact structures 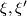 , respectively, this is equivalent to saying that
, respectively, this is equivalent to saying that  and
and 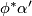 determine the same hyperplane field, and hence equivalent to the existence of a nowhere zero function
determine the same hyperplane field, and hence equivalent to the existence of a nowhere zero function 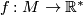 such that
such that 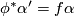 .
.
 where the function
where the function  is constant equal to
is constant equal to  . This is called a strict contactomorphism of the corresponding strict contact manifolds. In the example, the strict contactomorphism
. This is called a strict contactomorphism of the corresponding strict contact manifolds. In the example, the strict contactomorphism 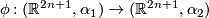 is given by
is given by 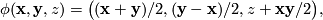
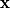 and
and 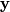 stand for
stand for 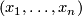 and
and 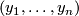 , respectively, and
, respectively, and 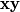 stands for
stands for 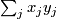 .
.
2.2 The standard contact structure on S2n+1
Let 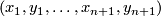 be Cartesian coordinates on
be Cartesian coordinates on 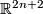 . Then the standard contact structure
. Then the standard contact structure 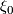 on the unit sphere
on the unit sphere 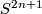 in
in 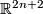 is given by the contact form
is given by the contact form
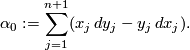
Write  for the radial coordinate on
for the radial coordinate on 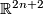 , that is,
, that is, 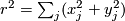 . One checks easily that
. One checks easily that 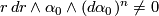 for
for 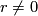 . Since
. Since 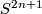 is a level set of
is a level set of  (or
(or 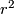 ), this verifies the contact condition. Alternatively, one may regard
), this verifies the contact condition. Alternatively, one may regard 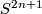 as the unit sphere in
as the unit sphere in 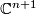 . Then the contact structure
. Then the contact structure 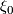 may be viewed as the hyperplane field of complex tangencies. Indeed, write
may be viewed as the hyperplane field of complex tangencies. Indeed, write  for the complex structure on
for the complex structure on 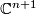 corresponding to the complex coordinates
corresponding to the complex coordinates 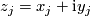 , that is,
, that is, 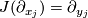 . Then
. Then
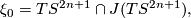
which means that 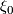 defines at each point
defines at each point 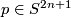 the
the  -invariant subspace of
-invariant subspace of 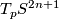 . Equation (1) follows from the observation that
. Equation (1) follows from the observation that 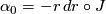 .
.
Here is a further example of contactomorphic manifolds.
Proposition 2.3.
For any point 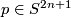 , the contact manifolds
, the contact manifolds 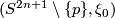 and
and 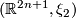 are contactomorphic.
are contactomorphic.
This is slightly less obvious than it may seem, since stereographic projection does not quite do the job. For a proof of this proposition, due to Erlandsson, see [Geiges2008, Proposition 2.1.8].
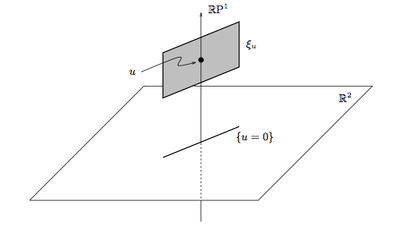
2.3 The space of contact elements
Let  be a smooth
be a smooth  -dimensional manifold. A contact element is a hyperplane in a tangent space to
-dimensional manifold. A contact element is a hyperplane in a tangent space to  . The space of contact elements of
. The space of contact elements of  is the collection of pairs
is the collection of pairs 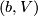 consisting of a point
consisting of a point 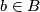 and a contact element
and a contact element 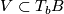 . This space of contact elements can be naturally identified with the projectivised cotangent bundle
. This space of contact elements can be naturally identified with the projectivised cotangent bundle 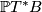 , by associating with a hyperplane
, by associating with a hyperplane 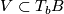 the linear map
the linear map 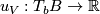 , well defined up to multiplication by a non-zero scalar, with
, well defined up to multiplication by a non-zero scalar, with 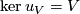 . The space
. The space 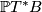 is a manifold of dimension
is a manifold of dimension 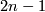 , and it carries a natural contact structure as defined in the following proposition.
, and it carries a natural contact structure as defined in the following proposition.
Proposition 2.4.
Write  for the bundle projection
for the bundle projection 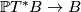 . For
. For 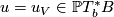 , let
, let 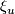 be the hyperplane in
be the hyperplane in 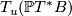 such that
such that 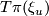 is the hyperplane
is the hyperplane  in
in 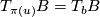 defined by
defined by  . Then
. Then  defines a contact structure on
defines a contact structure on 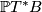 .
.
Figure 2 illustrates the construction for 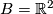 . Here
. Here 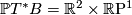 .
.
 be local coordinates on
be local coordinates on  , and
, and 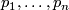 the corresponding dual coordinates in the fibres of the cotangent bundle
the corresponding dual coordinates in the fibres of the cotangent bundle 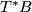 . This means that the coordinate description of covectors is given by
. This means that the coordinate description of covectors is given by 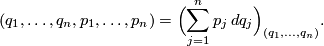
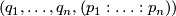
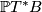 defines the hyperplane
defines the hyperplane 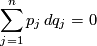
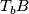 , where
, where 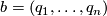 . By construction, the natural contact structure
. By construction, the natural contact structure  on
on 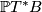 is defined by
is defined by
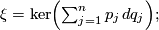
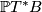 , although the
, although the  -form
-form 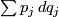 is not. In order to verify the contact condition for
is not. In order to verify the contact condition for  , we restrict to affine subspaces of the fibre. Over the open set
, we restrict to affine subspaces of the fibre. Over the open set 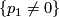 , for instance,
, for instance,  is defined in terms of affine coordinates
is defined in terms of affine coordinates 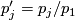 ,
, 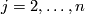 , by the equation
, by the equation 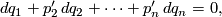
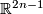 .
.

2.4 A non-coorientable contact structure
In the previous example, we now specialise to 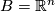 . Then the space of contact elements is
. Then the space of contact elements is 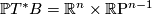 . In terms of Cartesian coordinates
. In terms of Cartesian coordinates 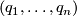 on
on  and homogeneous coordinates
and homogeneous coordinates 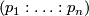 on
on 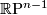 , the natural contact structure on this space of contact elements is now defined globally by equation (2). For
, the natural contact structure on this space of contact elements is now defined globally by equation (2). For  , and identifying
, and identifying 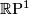 with
with 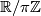 with coordinate
with coordinate 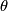 , this natural contact structure can be written as
, this natural contact structure can be written as
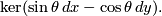
This is an example of a contact structure that is not coorientable. It lifts to a coorientable contact structure on 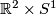 , given by the same equation, with
, given by the same equation, with 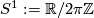 . Similar orientability issues arise for general
. Similar orientability issues arise for general  . Write
. Write 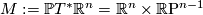 and
and  for the natural contact structure on this space of contact elements. We claim the following:
for the natural contact structure on this space of contact elements. We claim the following:
- If
 is even, then
is even, then  is orientable;
is orientable;  is neither orientable nor coorientable.
is neither orientable nor coorientable. - If
 is odd, then
is odd, then  is not orientable;
is not orientable;  is not coorientable, but it is orientable.
is not coorientable, but it is orientable.
The statement about orientability of  follows from the corresponding statement for
follows from the corresponding statement for 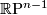 . The fact that
. The fact that  is never coorientable follows from the observation that
is never coorientable follows from the observation that 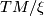 can be identified with the canonical line bundle on
can be identified with the canonical line bundle on 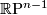 (pulled back to
(pulled back to  ), which is known to be non-trivial, see [Geiges2008, Proposition 2.1.13]. In case (i), since
), which is known to be non-trivial, see [Geiges2008, Proposition 2.1.13]. In case (i), since  is orientable but
is orientable but  not coorientable, it follows that
not coorientable, it follows that  cannot be orientable. The fact that in case (ii) the contact structure is orientable is the consequence of a more general statement in the next section.
cannot be orientable. The fact that in case (ii) the contact structure is orientable is the consequence of a more general statement in the next section.
2.5 More orientability issues
Notice that a contact manifold with a coorientable contact structure is always orientable (and so is the contact structure), because a globally defined contact form gives rise to a volume form on the manifold. This gives a quicker way to see that in our previous example for  odd the contact structure
odd the contact structure  cannot be coorientable. But even for contact structures that need not be coorientable one has the following:
cannot be coorientable. But even for contact structures that need not be coorientable one has the following:
- Any contact manifold of dimension
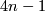 is naturally oriented.
is naturally oriented. - Any contact structure on a manifold of dimension
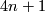 is naturally oriented.
is naturally oriented.
Statement (i) follows from the observation that the sign of the volume form 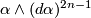 does not depend on the choice of (local)
does not depend on the choice of (local)  -form
-form  defining the contact structure. Similarly, in case (ii) the sign of
defining the contact structure. Similarly, in case (ii) the sign of 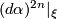 does not depend on the choice of
does not depend on the choice of  .
.
2.6 Three-dimensional contact manifolds
One can easily write down examples of contact structures on some closed  -manifolds. The
-manifolds. The  -sphere is dealt with in Section 2.2. The contact structure from equation (3) in Section 2.4 descends to a contact structure on the
-sphere is dealt with in Section 2.2. The contact structure from equation (3) in Section 2.4 descends to a contact structure on the  -torus
-torus 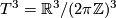 . On
. On 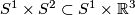 one has the contact structure
one has the contact structure 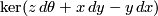 . Notice that by the previous section a
. Notice that by the previous section a  -dimensional contact manifold is necessarily orientable. In fact, as shown by Martinet [Martinet1971], this is the only restriction.
-dimensional contact manifold is necessarily orientable. In fact, as shown by Martinet [Martinet1971], this is the only restriction.
Theorem 2.5 [Martinet].
Every closed, orientable  -manifold admits a contact structure.
-manifold admits a contact structure.
2.7 Brieskorn manifolds
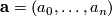 be an
be an 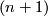 -tupel of integers
-tupel of integers 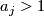 , and set
, and set 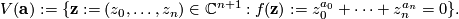
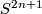 denoting the unit sphere in
denoting the unit sphere in 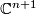 , we define
, we define 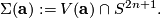
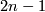 . Manifolds of this form are called Brieskorn manifolds [Brieskorn1966]. It can be shown that the standard contact form on
. Manifolds of this form are called Brieskorn manifolds [Brieskorn1966]. It can be shown that the standard contact form on 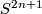 induces a contact structure on
induces a contact structure on 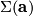 . This has been observed independently by Abe-Erbacher, Lutz-Meckert and Sasaki-Hsü, cf. [Geiges2008, Section 7.1].
. This has been observed independently by Abe-Erbacher, Lutz-Meckert and Sasaki-Hsü, cf. [Geiges2008, Section 7.1].
3 A brief history of the terminology
The concept of a contact element first appeared in systematic form in 1896 in the work of Sophus Lie [Lie1896]. His terminology was a little more specific, for instance, a contact element of the plane was called a line element (Linienelement). A contact transformation (Berührungstransformation) for Lie was defined as above, but he only considered this in the context of spaces of contact elements and their natural contact structure (which did not yet bear that name). Such contact transformations play a significant role in the work of E. Cartan, E. Goursat, H. Poincaré and others in the second half of the 19th century. For instance, the Legendre transformation in classical mechanics is a contact transformation. The study of contact manifolds in the modern sense can be traced back to the work of Georges Reeb [Reeb1952], who referred to a strict contact manifold 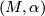 as a `système dynamique avec invariant intégral de Monsieur Elie Cartan'. The relation with dynamical systems comes from the fact that a contact form
as a `système dynamique avec invariant intégral de Monsieur Elie Cartan'. The relation with dynamical systems comes from the fact that a contact form  gives rise to a vector field
gives rise to a vector field  defined uniquely by the equations
defined uniquely by the equations
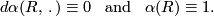
This vector field is nowadays called the Reeb vector field of  . The words `contact structure' and `contact manifold' seem to make their first appearance in the work of Boothby-Wang [Boothby&Wang1958], Gray [Gray1959] and Kobayashi [Kobayashi1959] in the late 1950s. For more historical information on contact manifolds see [Lutz1988] and [Geiges2001].
. The words `contact structure' and `contact manifold' seem to make their first appearance in the work of Boothby-Wang [Boothby&Wang1958], Gray [Gray1959] and Kobayashi [Kobayashi1959] in the late 1950s. For more historical information on contact manifolds see [Lutz1988] and [Geiges2001].
4 References
- [Boothby&Wang1958] W. M. Boothby and H. C. Wang, On contact manifolds, Ann. of Math. (2) 68 (1958), 721–734. MR0112160 (22 #3015) Zbl 0084.39204
- [Brieskorn1966] E. Brieskorn, Beispiele zur Differentialtopologie von Singularitäten, Invent. Math. 2 (1966), 1–14. MR0206972 (34 #6788) Zbl 0145.17804
- [Geiges2001] H. Geiges, A brief history of contact geometry and topology, Expo. Math. 19 (2001), 25–53. MR1820126 (2002c:53129) Zbl 1048.53001
- [Geiges2008] H. Geiges, An introduction to contact topology, Cambridge Stud. Adv. Math. 109, Cambridge University Press, 2008. MR2397738 (2008m:57064) Zbl 1153.53002
- [Gray1959] J. W. Gray, Some global properties of contact structures, Ann. of Math. (2) 69 (1959), 421–450. MR0112161 (22 #3016) Zbl 0092.39301
- [Kobayashi1959] S. Kobayashi, Remarks on complex contact manifolds, Proc. Amer. Math. Soc. 10 (1959), 164–167. MR0111061 (22 #1925) Zbl 0090.38502
- [Lie1896] S. Lie, Geometrie der Berührungstransformationen (dargestellt von S. Lie und G. Scheffers), B. G. Teubner, Leipzig, 1896. MR0460049 (57 #45) Zbl 03630675
- [Lutz1988] R. Lutz, Quelques remarques historiques et prospectives sur la géométrie de contact, in: Conference on Differential Geometry and Topology, (Sardinia, 1988) Rend. Sem. Fac. Sci. Univ. Cagliari 58 (1988), no.suppl., 361–393. MR1122864 (93b:53025)
- [Martinet1971] J. Martinet, Formes de contact sur les variétés de dimension
 , Proc. Liverpool Singularities Sympos. II, Lecture Notes in Math. 209, Springer-Verlag, Berlin (1971), 142–163. MR0350771 (50 #3263) Zbl 0215.23003
, Proc. Liverpool Singularities Sympos. II, Lecture Notes in Math. 209, Springer-Verlag, Berlin (1971), 142–163. MR0350771 (50 #3263) Zbl 0215.23003
- [Reeb1952] G. Reeb, Sur certaines propriétés topologiques des trajectoires des systèmes dynamiques, Acad. Roy. Belgique. Cl. Sci. Mém. Coll. in 8
 27, no.9 (1952). MR0058202 (15,336b) Zbl 0048.32903
27, no.9 (1952). MR0058202 (15,336b) Zbl 0048.32903
5 External links
- The Encyclopedia of Mathematics article on contact structure
- The Wikipedia page about contact geometry