3-manifolds
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
In the 3-dimensional setting there is no distinction between smooth, PL and topological manifolds neccesary; the categories of smooth, PL and topological manifolds are equivalent (TODO ref). A lot of techniques have been developed in the last century to study 3-manifolds but most of them are very special and don't generalise to higher dimensions. One key idea is to decompose manifolds along incompressible surfaces into smaller pieces, to which certain geometric models apply. A great progress was made in with the proof of the Poincaré conjecture and Thurton's geometrization conjecture by Perelman in 2003.
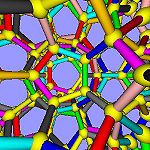
 - here a view of the induced tesselation
- here a view of the induced tesselation[edit] 2 Construction and examples
Basic examples are 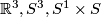 with
with 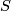 any surface.
Important types of 3-manifolds are Haken-Manifolds, Seifert-Manifolds, 3-dimensional lens spaces, Torus-bundles and Torus semi-bundles.
any surface.
Important types of 3-manifolds are Haken-Manifolds, Seifert-Manifolds, 3-dimensional lens spaces, Torus-bundles and Torus semi-bundles.
There are two topological processes to join 3-manifolds to get a new one.
The first is the connected sum of two manifolds  and
and 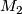 . Choose embeddings
. Choose embeddings 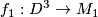 and
and 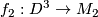 , remove the interior of
, remove the interior of 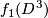 and
and 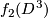 and glue
and glue  and
and 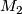 together along the boundaries
together along the boundaries 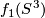 and
and 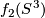 .
The second uses incompressible surfaces. Let
.
The second uses incompressible surfaces. Let  be manifold and
be manifold and 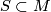 a surface.
a surface. 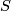 is incompressible, if there is no disk
is incompressible, if there is no disk 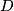 in
in  with
with 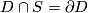 .
The torus sum is the process which glues incompressible tori boundary components together.
.
The torus sum is the process which glues incompressible tori boundary components together.
(TODO What is incompressibility needed? / What is is good for/ What happen if one takes a compressible surface ?)
[edit] 3 Invariants
In the 3-dimensional world the fundamental group is a powerful invariant to distiguish manifolds. It determines already all homology groups:
-
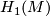 = abelization of
= abelization of 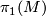 .
.
-
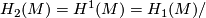 torsion
torsion
-
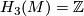
-
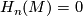 for
for 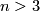
[edit] 4 Classification/Characterization
By reversing the process of connected and torus sum every 3-manifold can be decomposed into pieces which admit a geometric structure. We describe the details in the following.
[edit] 4.1 Prime decomposition
Definition 4.1.
A manifold  is called prime, if it can't be written as a non-trivial connected sum, i.e.
is called prime, if it can't be written as a non-trivial connected sum, i.e. 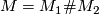 implies
implies 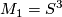 or
or 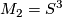 .
A manifold
.
A manifold  is called irreducible if every embedded
is called irreducible if every embedded  bounds a ball, i.e. the embedding extends to an embedding of
bounds a ball, i.e. the embedding extends to an embedding of 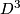
Irreducibility is only slightly stronger than being prime. A orientable prime 3-manifold is either 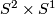 or every embedded 2-sphere bounds a ball.
or every embedded 2-sphere bounds a ball.
Theorem 4.2 Kneser.
Every orientable, compact 3-manifold  has a decomposition
has a decomposition 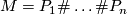 into prime manifolds
into prime manifolds 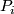 unique up to ordering and
unique up to ordering and  summands.
summands.
A orientable prime 3-manifold is either 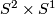 or every embedded 2-sphere bounds a ball, in which case the manifold is called irreducible.
or every embedded 2-sphere bounds a ball, in which case the manifold is called irreducible.
Van Kampen's theorem tells you, that 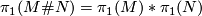 . Hence any 3-manifold, whose fundamental group cannot be written as a free product of two nontrivial subgroups, can only be written as the connected sum of another 3-manifold with a simply connected 3-manifold. By the Poincaré conjecture a simply connected 3-manifold is already homeomorphic to
. Hence any 3-manifold, whose fundamental group cannot be written as a free product of two nontrivial subgroups, can only be written as the connected sum of another 3-manifold with a simply connected 3-manifold. By the Poincaré conjecture a simply connected 3-manifold is already homeomorphic to  . Hence each such manifold is prime.
. Hence each such manifold is prime.
Prime 3-manifolds can be distinguished by their fundamental groups into the following 3 types:
[edit] 4.1.1 Type I: finite fundamental group
The universal cover 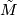 is a simply-connected 3-manifold. As the fundamental group already determines the homology of a oriented, closed compact 3-manifold, it has to be a homology sphere. Using the Hurewicz-theorem, its fundamental class is represented by a degree 1 map
is a simply-connected 3-manifold. As the fundamental group already determines the homology of a oriented, closed compact 3-manifold, it has to be a homology sphere. Using the Hurewicz-theorem, its fundamental class is represented by a degree 1 map 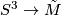 . This map induces isomorphisms on the homology and on the fundamental group. Hence it is a weak homotopy equivalence, and hence a homotopy equivalence by Whitehead's theorem (ref?).
Hence every prime
. This map induces isomorphisms on the homology and on the fundamental group. Hence it is a weak homotopy equivalence, and hence a homotopy equivalence by Whitehead's theorem (ref?).
Hence every prime  -manifold with finite fundamental group arises as the quotient of a homotopy sphere by a free action of a finite group.
With the use of the Poincaré conjecture every homotopy 3-sphere is homeomorphic to
-manifold with finite fundamental group arises as the quotient of a homotopy sphere by a free action of a finite group.
With the use of the Poincaré conjecture every homotopy 3-sphere is homeomorphic to  and we can write
and we can write 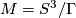 . If
. If  is cyclic
is cyclic  is known as lens space (ref).
is known as lens space (ref).
[edit] 4.1.2 Type II: infinite cyclic fundamental group
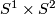 is the only orientable closed prime 3-manifold of this type. Futhermore it is the only not irreducible prime manifold. (TODO: proof/ref)
is the only orientable closed prime 3-manifold of this type. Futhermore it is the only not irreducible prime manifold. (TODO: proof/ref)
[edit] 4.1.3 Type III: infinite non-cyclic fundamental group
Such a manifold  is always aspherical (TODO ref). The sphere theorem states, that every map
is always aspherical (TODO ref). The sphere theorem states, that every map 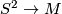 is homotopic to an embedding; and - as
is homotopic to an embedding; and - as  is irreducible - it is nullhomotopic. Hence
is irreducible - it is nullhomotopic. Hence 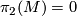 . Consider the universal covering
. Consider the universal covering 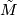 of
of  . Its first homology vanishes as it is simply connected. The long exact sequence of homotopy groups of the fibration
. Its first homology vanishes as it is simply connected. The long exact sequence of homotopy groups of the fibration 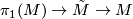 gives a isomorphism
gives a isomorphism 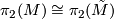 . Hence by Hurewicz' theorem
. Hence by Hurewicz' theorem 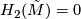 . Furthermore
. Furthermore 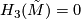 , as
, as  is noncompact. Applying Hurewicz theorem again we get that all homotopy groups of
is noncompact. Applying Hurewicz theorem again we get that all homotopy groups of 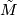 vanish and hence by Whitehead's theorem
vanish and hence by Whitehead's theorem 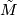 is contractible. This means that
is contractible. This means that  is apherical.
Hence the homotopy type of a prime 3-manifold with infinite non-cyclic fundamental group is uniquely determined by its fundamental group.
Furthermore not every group can occur as a fundamental group of a prime 3-manifold. The equivariant cellular chain complex of
is apherical.
Hence the homotopy type of a prime 3-manifold with infinite non-cyclic fundamental group is uniquely determined by its fundamental group.
Furthermore not every group can occur as a fundamental group of a prime 3-manifold. The equivariant cellular chain complex of 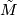 is a projective resolution of the trivial
is a projective resolution of the trivial ![\Zz[\pi_1(M)]](/images/math/0/5/b/05b367770d614ae3efd04bd7bd86ee21.png) -module
-module  . Hence ....
For any subgroup
. Hence ....
For any subgroup 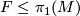 the space
the space 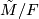 is a finite-dimensional model for
is a finite-dimensional model for 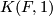 . For example a finite group cannot have such a model (by group homology ref) and hence
. For example a finite group cannot have such a model (by group homology ref) and hence 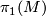 must be torsionfree. Furthermore it is a Poincaré duality group (link).
must be torsionfree. Furthermore it is a Poincaré duality group (link).
[edit] 4.2 Torus decomposition
According to the previous section it remains to classify irreducible prime 3-manifolds. After cutting along spheres which don't bound balls as far as possible the next canonical step is to consider incompressible tori which are disjoint from the boundary.
Theorem 4.3 Jacob-Shalen, Johannson.
If  is an irreducible compact orientable manifold, then there is a collection of disjoint incompressible tori
is an irreducible compact orientable manifold, then there is a collection of disjoint incompressible tori 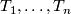 in
in  such that splitting
such that splitting  along the union of these tori produces manifolds
along the union of these tori produces manifolds 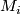 which are either Seifert-fibered or atoroidal, i.e. every incompressible torus in
which are either Seifert-fibered or atoroidal, i.e. every incompressible torus in 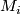 is isotopic to a torus component of
is isotopic to a torus component of 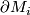 . Furthermore, a minimal such collection of tori
. Furthermore, a minimal such collection of tori 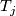 is unique up to isotopy in
is unique up to isotopy in  .
.
Thurston's geometrization conjectures states that all the pieces we get by this JSJ-decomposition admit one of eight possible geometric structures:
There is a list of eight simply connected Riemannian manifolds - the so called model geometries. A geometric structure on  is the choice of a Riemannian metric on
is the choice of a Riemannian metric on  , with the property that its universal covering
, with the property that its universal covering 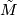 equipped with the pull-back metric is isometric to one of the eight model geometries. It might a priori be easier to classify all cocompact actions on the several model geometries.
equipped with the pull-back metric is isometric to one of the eight model geometries. It might a priori be easier to classify all cocompact actions on the several model geometries.
The Seifert-fibered pieces are well understood since the work of Seifert in the 30s (TODO: mention classification theorem). The atoroidal pieces are described by the following Hyperbolization theorem which was stated by Thurston (ref) and proven by Perelman. \begin{thm} Every irreducible atoroidal closed 3-manifold that is not Seifert-fibred is hyperbolic. \end{thm}
[edit] 4.3 Dehn surgery
Dehn surgery is a way of constructing (TODO oriented ? neccesary) 3-manifolds. Given a link in a  -manifold
-manifold 
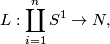
and a choice of a tubular neighborhood of 
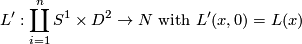
(This choice essentially is the choice of a trivialization of the normal bundle; TODO find a correct formulation for this).
This gives us a family of embedded, disjoint, full tori. The idea of Dehn surgery is to remove these Tori and glue them back in using a twist.\\
Let us restrict to the case with only one solid torus 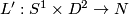 .
Choose any self-homeomorphism
.
Choose any self-homeomorphism  of the torus
of the torus 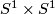 . The result of the Dehn surgery at
. The result of the Dehn surgery at  with the twist
with the twist  is defined as
is defined as
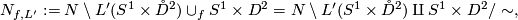
where the equivalence relation identifies for 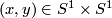 the points
the points 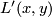 in the left component and
in the left component and 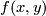 in the right component.
If
in the right component.
If  is the coordinate flipping, Dehn surgery is nothing but usual codimension
is the coordinate flipping, Dehn surgery is nothing but usual codimension  surgery.
surgery.
Lemma 4.4.
Suppose  are isotopic and let
are isotopic and let 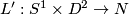 be any embedding of the full Torus in a
be any embedding of the full Torus in a  -Manifold
-Manifold  .Then
.Then 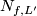 and
and 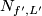 are homeomorphic.
are homeomorphic.
Proof.
Let ![j:T^2\times [0;1] \rightarrow T^2](/images/math/d/d/8/dd86a75e185c60c9e15817514bf6720b.png) be an isotopy from
be an isotopy from  to
to  . This gives a homeomorphism:
. This gives a homeomorphism:
![\displaystyle J:T^2\times [0;1]\rightarrow T^2\times [0;1] \qquad (x,y,t)\mapsto (j(x,y,t),t).](/images/math/0/4/b/04b7312959834676f44da972c9809dbe.png)
(TODO: is its inverse 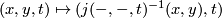 continuous ?).
The idea is to grab some additional space, where one can use the map
continuous ?).
The idea is to grab some additional space, where one can use the map 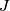 . TODO
. TODO

TODO formulate a lemma, that M_{f,L'} also only depends on the isotopy class of 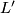 (which is hopefully true).
Hence, we have to classify all self-homeomorphisms of
(which is hopefully true).
Hence, we have to classify all self-homeomorphisms of 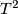 up to isotopy.
up to isotopy.
Lemma 4.5.
Every self-homeomorphism of 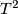 is isotopic to exactly one homeomorphism of the shape
is isotopic to exactly one homeomorphism of the shape
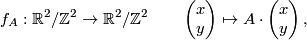
where 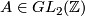 (reference of proof).
(reference of proof).
Proof. Since the torus is a 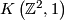 -space, we have that
-space, we have that 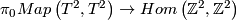 is an isomorphism. Homotopic surface homeomorphisms are isotopic (Reference?). Thus the restriction
is an isomorphism. Homotopic surface homeomorphisms are isotopic (Reference?). Thus the restriction 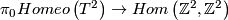 is injective. Moreover, each
is injective. Moreover, each 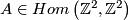 is realised by
is realised by 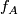 , therefore
, therefore 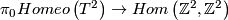 is also surjective.
TODO find a reference in ANY source about the mapping class group
is also surjective.
TODO find a reference in ANY source about the mapping class group

The next lemma tells us, that composition of self-homeomorphisms corresponds to two successive Dehn surgeries.
Lemma 4.6.
Let 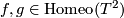 be given and let
be given and let 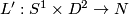 is an embedding of the full torus in a 3-manifold. Then we have map
is an embedding of the full torus in a 3-manifold. Then we have map
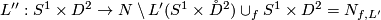
given by the map 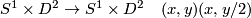 postcomposed with the canonical inclusion in the second coordinate.
Then
postcomposed with the canonical inclusion in the second coordinate.
Then 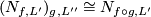 . TODO right order of composition ? We will see in the proof.
. TODO right order of composition ? We will see in the proof.
Proof.

We have to find out, which self-homeomorphisms of the torus don't change the homeomorphism type of the manifold.
Lemma 4.7. Consider a matrix of the form 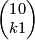 and let
and let 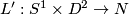 be any eembedding. Then
be any eembedding. Then 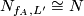 .
.
TODO are there any orientation reversing homeos, that also extend ? Think so. Also add them here.
Proof.
The homeomorphism 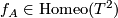 extends to a homeomorphism of
extends to a homeomorphism of 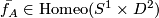 :
:
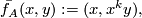
where 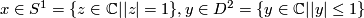 .
Using this homeomorphism one can define a homeomorphism from
.
Using this homeomorphism one can define a homeomorphism from 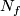 to
to  :
:
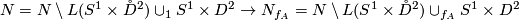
given by the identity on the left component and 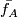 on the right component.
on the right component.

Together with (link to comment about composition), this tells us, that 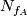 really only depends on the coset
really only depends on the coset 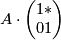 (TODO check right or left coset). This coset is uniquely determined by the image
(TODO check right or left coset). This coset is uniquely determined by the image 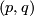 of
of 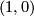 with
with  and
and  coprime.
coprime.
The ratio 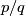 is called the surgery coefficient. (TODO what is the quotient good for ?)<++>
is called the surgery coefficient. (TODO what is the quotient good for ?)<++>
TODO does the result give different manifolds.
TODO does the result only depend on the isotopy class of the link.
Every compact (oriented /able, neccesary ?) 3-manifold might be obtained from  by a Dehn surgery along a link (TODO ref). Of course this does not satisfy to classify 3-manifolds without having a good classification of links in
by a Dehn surgery along a link (TODO ref). Of course this does not satisfy to classify 3-manifolds without having a good classification of links in  .
.
[edit] 5 References
[Scott1983], [Thurston1997], [Hatcher2000], [Hempel1976]
- [Hatcher2000] A. Hatcher, Basic Topology of 3-Manifolds, Unpublished notes.
- [Hempel1976] J. Hempel,
 -Manifolds, Princeton University Press, Princeton, N. J., 1976. MR0415619 (54 #3702) Zbl 1058.57001
-Manifolds, Princeton University Press, Princeton, N. J., 1976. MR0415619 (54 #3702) Zbl 1058.57001
- [Scott1983] P. Scott, The geometries of
 -manifolds, Bull. London Math. Soc. 15 (1983), no.5, 401–487. MR705527 (84m:57009) Zbl 0662.57001
-manifolds, Bull. London Math. Soc. 15 (1983), no.5, 401–487. MR705527 (84m:57009) Zbl 0662.57001
- [Thurston1997] W. P. Thurston, Three-dimensional geometry and topology. Vol. 1, Princeton University Press, Princeton, NJ, 1997. MR1435975 (97m:57016) Zbl 0873.57001