Unoriented bordism
|
The user responsible for this page is Matthias Kreck. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
We denote the unoriented bordism groups by 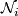 . The sum of these groups
. The sum of these groups
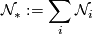
forms a ring under cartesian products of manifolds. Thom [Thom1954] has shown that this ring is a polynomial ring over 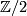 in variables
in variables 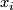 for
for 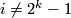 and he has shown that for
and he has shown that for  even one can take
even one can take 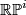 for
for 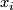 . Dold [Dold1956] has constructed manifolds for
. Dold [Dold1956] has constructed manifolds for 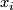 with
with  odd.
odd.
2 Construction and examples
Dold constructs certain bundles over 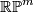 with fibre
with fibre 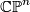 denoted by
denoted by
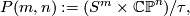
 is the involution mapping
is the involution mapping ![(x,[y])](/images/math/5/f/4/5f4498f04b89f91ead4518908defc4a5.png) to
to ![(-x, [\bar y])](/images/math/d/b/a/dba628c4f8c13c856cc15d4ca98d20dd.png) and
and 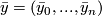 for
for 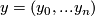 . These manifolds are now called Dold manifolds.
. These manifolds are now called Dold manifolds.
Using the results by Thom [Thom1954] Dold shows that these manifolds give ring generators of 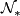 .
.
Theorem (Dold) [Dold1956] 2.1. For  even set
even set ![x_i:= [P(i,0) ]= [\mathbb {RP}^i]](/images/math/2/2/5/2250cfd96e997d9e77c02cd1f8924c10.png) and for
and for 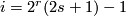 set
set ![x_i:=[ P(2^r-1,s2^r)]](/images/math/1/a/9/1a986852c3a89589a1d866eeb35d3bbc.png) . Then for
. Then for 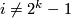
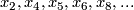
are polynomial generators of 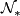 olver
olver 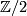 :
:
![\displaystyle \mathcal N_* \cong \mathbb Z/2[x_2,x_4,x_5,x_6,x_8...].](/images/math/b/2/8/b2808ca7f9cef2cc7632e4d8c8d31bd2.png)
3 Invariants
To prove the Theorem Dold has to compute the characteristic numbers which according to Thom's theorem determine the bordism class. As a first step Dold computes the cohomology ring with 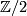 -coeffcients. The fibre bundle
-coeffcients. The fibre bundle 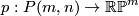 has a section
has a section ![s([x]) := [(x,[1,...,1])]](/images/math/8/e/4/8e485f68ce413f54b22caf2aab93ce29.png) and we consider the cohomology classes (always with
and we consider the cohomology classes (always with 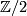 -coefficients)
-coefficients)
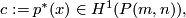
where  is a generator of
is a generator of 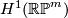 , and
, and
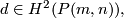
which is characterized by the property that the restriction to a fibre is non-trivial and 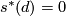 .
.
Theorem [Dold1956] 3.1. The classes 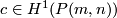 and
and 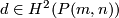 generate
generate 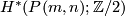 with only the relations
with only the relations
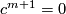
and
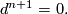
The Steenrod squares act by
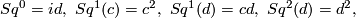
and all other Squares 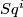 act trivially on
act trivially on  and
and  . On the decomposable classes the action is given by the Cartan formula.
. On the decomposable classes the action is given by the Cartan formula.
The total Stiefel-Whitney class of the tangent bundle is
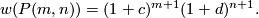
4 Classification
To give explicit polynomial generators is useful information, if one wants to prove a formula like for example that ![<w_n(M),[M]> = e(M)\,\, mod\,\, 2](/images/math/f/9/7/f979812bcd6e4e9da8b28d155dc2a5bd.png) , where
, where 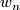 is the
is the  -th Stiefel-Whitney class of an
-th Stiefel-Whitney class of an  -dimensional manifold and
-dimensional manifold and 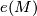 is the Euler characteristic, which one has to check on generators. But it does not help to classify manifolds up to bordism. There is an explicit answer to this question by Thom:
is the Euler characteristic, which one has to check on generators. But it does not help to classify manifolds up to bordism. There is an explicit answer to this question by Thom:
Theorem [Thom1954] 4.1. Two closed  -manifolds
-manifolds  and
and  are bordant if and only if all Stiefel-Whitney numbers agree:
are bordant if and only if all Stiefel-Whitney numbers agree:
![\displaystyle <w_{i_1}\cup....\cup w_{i_k}(M), [M]> = <w_{i_1}\cup....\cup w_{i_k}(N), [N]>](/images/math/d/1/0/d10c5e54476446995c8b94e52914f356.png)
for all partitions 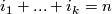 .
.
5 Further discussion
For 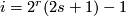 odd
odd 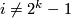 the manifolds
the manifolds 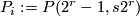 are orientable and thus after choosing an orientation give an element in the oriented bordism group
are orientable and thus after choosing an orientation give an element in the oriented bordism group 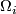 . Since
. Since 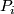 admits an obvious orientation reversing diffeomorphism, these elements are
admits an obvious orientation reversing diffeomorphism, these elements are  -torsion. Thus we obtain a subring in
-torsion. Thus we obtain a subring in 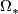 isomorphic to
isomorphic to ![\mathbb Z/2[x_5, x_9, x_{11},...]](/images/math/3/f/5/3f5eba8201390e525a11c5bc73618688.png) . For more information about
. For more information about 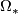 see the page on oriented bordism.
see the page on oriented bordism.
6 References
- [Dold1956] A. Dold, Erzeugende der Thomschen Algebra
 , Math. Z. 65 (1956), 25–35. MR0079269 (18,60c) Zbl 0071.17601
, Math. Z. 65 (1956), 25–35. MR0079269 (18,60c) Zbl 0071.17601
- [Thom1954] R. Thom, Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28 (1954), 17–86. MR0061823 (15,890a) Zbl 0057.15502