Unoriented bordism
|
The user responsible for this page is Matthias Kreck. No other user may edit this page at present. |
Contents |
1 Introduction
We denote the non-oriented bordism groups by 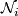 . The sum of these groups
. The sum of these groups
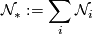
are a ring under cartesian products of the manifolds. Thom [Thom] has shown that this ring is a polynomial ring over 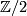 in variables
in variables 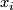 for
for 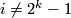 and he has shown that for
and he has shown that for  even one can take
even one can take 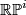 for
for 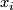 . Dold [Dold1956] has constructed manifolds for
. Dold [Dold1956] has constructed manifolds for 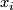 with
with  odd.
odd.
2 Construction and examples
Dold constructs certain bundles over 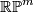 with fibre
with fibre 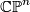 denoted by
denoted by
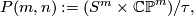
 is the involution mapping
is the involution mapping ![(x,[y])](/images/math/5/f/4/5f4498f04b89f91ead4518908defc4a5.png) to
to ![(-x, [\bar y])](/images/math/d/b/a/dba628c4f8c13c856cc15d4ca98d20dd.png) and
and 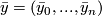 for
for 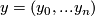 . These manifolds are now cold Dold manifolds.
. These manifolds are now cold Dold manifolds.
Using the results by Thom [Thom1954] Dold shows that these manifolds give ring generators of 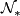 .
.
Theorem (Dold) [Dold1956] 2.1. For  even set
even set ![x_i:= [P(i,0) ]= [\mathbb {RP}^i]](/images/math/2/2/5/2250cfd96e997d9e77c02cd1f8924c10.png) and for
and for 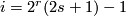 set
set ![x_i:=[ P(2^r-1,s2^r)]](/images/math/1/a/9/1a986852c3a89589a1d866eeb35d3bbc.png) . Then for
. Then for 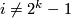
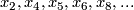
are polynomial generators of 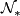 olver
olver 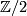 :
:
![\displaystyle \mathcal N_* \cong \mathbb Z/2[x_2,x_4,x_5,x_6,x_8...].](/images/math/b/2/8/b2808ca7f9cef2cc7632e4d8c8d31bd2.png)
3 Invariants
YOUR TEXT HERE ...
4 Classification/Characterization (if available)
YOUR TEXT HERE ...
5 Further discussion
YOUR TEXT HERE ...
6 References
- [Dold1956] A. Dold, Erzeugende der Thomschen Algebra
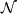 , Math. Z. 65 (1956), 25–35. MR0079269 (18,60c) Zbl 0071.17601
, Math. Z. 65 (1956), 25–35. MR0079269 (18,60c) Zbl 0071.17601
- [Thom] Template:Thom
- [Thom1954] R. Thom, Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28 (1954), 17–86. MR0061823 (15,890a) Zbl 0057.15502
|
This page has not been refereed. The information given here might be incomplete or provisional. |