Tangential homotopy equivalences (Ex)
(Difference between revisions)
m |
m |
||
| Line 4: | Line 4: | ||
# Give an example of a tangential homotopy equivalence which is not homotopic to a diffeomorphism. | # Give an example of a tangential homotopy equivalence which is not homotopic to a diffeomorphism. | ||
# Show that if $f \colon M \to N$ is a tangential homotopy equivelance, then there is a diffeomorphism | # Show that if $f \colon M \to N$ is a tangential homotopy equivelance, then there is a diffeomorphism | ||
| − | $$ F \colon D^n \times M \cong D^n \times N | + | $$ F \colon D^n \times M \cong D^n \times N$$ |
| + | such that $p_n \circ F|_{0 \times M}$ is homotopic to $f$, where $p_N \colon D^n \times N \to N$ is the projection. | ||
{{endthm}} | {{endthm}} | ||
</wikitex> | </wikitex> | ||
Revision as of 23:51, 25 August 2013
A homotopy equivalence 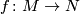 of closed smooth
of closed smooth  -manifolds is called tangential if
-manifolds is called tangential if 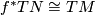 ; i.e.
; i.e.  pulls back the tangent bundle of
pulls back the tangent bundle of  to
to  .
.
Example 0.1.
- Give an example of a tangential homotopy equivalence which is not homotopic to a diffeomorphism.
- Show that if
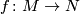 is a tangential homotopy equivelance, then there is a diffeomorphism
is a tangential homotopy equivelance, then there is a diffeomorphism
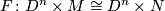
such that 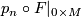 is homotopic to
is homotopic to  , where
, where 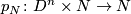 is the projection.
is the projection.