Talk:Three dimensional Heisenberg group (Ex)
(Difference between revisions)
Josh Howie (Talk | contribs) (Created page with "<wikitex>; Let $T$ be a torus and let $y$ and $z$ be generators of $\pi_1(T)\cong\mathbb{Z}\oplus\mathbb{Z}$. Let $f:T\rightarrow T$ be a homeomorphism of the torus such that ...") |
Josh Howie (Talk | contribs) |
||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
Let $T$ be a torus and let $y$ and $z$ be generators of $\pi_1(T)\cong\mathbb{Z}\oplus\mathbb{Z}$. Let $f:T\rightarrow T$ be a homeomorphism of the torus such that $f_*(y)=yz^{-1}$ and $f_*(z)=z$ (ie. $f$ is a Dehn twist.) Let $M$ be a torus bundle over $S^1$ with monodromy $f$. Then $\pi_1(M)$ is an HNN extension of $\pi_1(T)$ and we can write down a presentation | Let $T$ be a torus and let $y$ and $z$ be generators of $\pi_1(T)\cong\mathbb{Z}\oplus\mathbb{Z}$. Let $f:T\rightarrow T$ be a homeomorphism of the torus such that $f_*(y)=yz^{-1}$ and $f_*(z)=z$ (ie. $f$ is a Dehn twist.) Let $M$ be a torus bundle over $S^1$ with monodromy $f$. Then $\pi_1(M)$ is an HNN extension of $\pi_1(T)$ and we can write down a presentation | ||
| − | $\pi_1(M) = | + | $\pi_1(M) = \langle x,y,z \mid x^{-1}yx=yz^{-1}, x^{-1}zx=z, [y,z]=1\rangle$, with stable letter $x$. |
This is equivalent to the given presentation of the Heisenberg group. Therefore $M$ is the desired closed, orientable $3$-manifold. | This is equivalent to the given presentation of the Heisenberg group. Therefore $M$ is the desired closed, orientable $3$-manifold. | ||
</wikitex> | </wikitex> | ||
[[Category:Exercises]] | [[Category:Exercises]] | ||
[[Category:Exercises with solution]] | [[Category:Exercises with solution]] | ||
Revision as of 12:48, 7 January 2019
Let  be a torus and let
be a torus and let  and
and  be generators of
be generators of 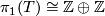 . Let
. Let 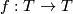 be a homeomorphism of the torus such that
be a homeomorphism of the torus such that 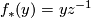 and
and 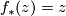 (ie.
(ie.  is a Dehn twist.) Let
is a Dehn twist.) Let  be a torus bundle over
be a torus bundle over  with monodromy
with monodromy  . Then
. Then 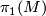 is an HNN extension of
is an HNN extension of 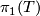 and we can write down a presentation
and we can write down a presentation
![\pi_1(M) = \langle x,y,z \mid x^{-1}yx=yz^{-1}, x^{-1}zx=z, [y,z]=1\rangle](/images/math/7/6/6/76677bebcc1537fc66bae4695bf9746d.png) , with stable letter
, with stable letter  .
This is equivalent to the given presentation of the Heisenberg group. Therefore
.
This is equivalent to the given presentation of the Heisenberg group. Therefore  is the desired closed, orientable
is the desired closed, orientable  -manifold.
-manifold.