Talk:Sphere bundles and spin (Ex)
Patrickorson (Talk | contribs) |
Patrickorson (Talk | contribs) |
||
| Line 12: | Line 12: | ||
m>4\implies x\in\pi_2(M)\quad &\text{can be embedded}\end{aligned}$$Hence we take an embedded sphere $\Sigma$ on which $w_2(M)$ does not vanish and call this the ''weird sphere''. Then this $\Sigma$ must have twisted normal bundle. Consider that for our untwisted surgery, $S^1$ must initially bound a disk and we can extend the normal framing of $S^1$ to the normal framing on $D^2$ (which is necessarily trivial). For the twisted surgery, $S^1$ must have the ''other'' framing. Take the $D^2$ bounded by $S^1$ to be inside a hemisphere of the weird sphere. Now form an isotopy moving $S^1$ from one hemisphere to the other of the weird sphere. This must necessarily exchange the framing we have on $S^1$ from trivial to twisted as the normal bundle of the weird sphere is twisted. However, the surgery at either end of an isotopy gives a diffeomorphic effect.<br /><br /> | m>4\implies x\in\pi_2(M)\quad &\text{can be embedded}\end{aligned}$$Hence we take an embedded sphere $\Sigma$ on which $w_2(M)$ does not vanish and call this the ''weird sphere''. Then this $\Sigma$ must have twisted normal bundle. Consider that for our untwisted surgery, $S^1$ must initially bound a disk and we can extend the normal framing of $S^1$ to the normal framing on $D^2$ (which is necessarily trivial). For the twisted surgery, $S^1$ must have the ''other'' framing. Take the $D^2$ bounded by $S^1$ to be inside a hemisphere of the weird sphere. Now form an isotopy moving $S^1$ from one hemisphere to the other of the weird sphere. This must necessarily exchange the framing we have on $S^1$ from trivial to twisted as the normal bundle of the weird sphere is twisted. However, the surgery at either end of an isotopy gives a diffeomorphic effect.<br /><br /> | ||
| − | To see this last part a different way, we may take a cylinder $M\times [0,1]$. This induces a trivial isotopy of the embedded $S^1$. At some $t\in[0,1]$, take a connect sum with the weird sphere and the isotopy $S^1\times[0,1]$. | + | To see this last part a different way, we may take a cylinder $M\times [0,1]$. This induces a trivial isotopy of the embedded $S^1$. At some $t\in[0,1]$, take a connect sum with the weird sphere and the isotopy $S^1\times[0,1]$. Now make the $S^1$ slide along the tube and then over the weird sphere and down to the bottom of the tube as $t$ increases from 0 to 1. This is not an isotopy but is now a concordance. However, within codimension $>3$ we can improve a concordance to an isotopy.<br /><br /> |
This does not cover the case $m=4$, I think it is still possible here but I don't have the solution. | This does not cover the case $m=4$, I think it is still possible here but I don't have the solution. | ||
</wikitex> | </wikitex> | ||
Revision as of 23:11, 29 March 2012
This is a standard clutching construction. Fix
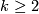 and suppose we have a linear
and suppose we have a linear 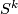 bundle
bundle  over the sphere
over the sphere 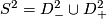 . A fibre bundle over a contractible space is trivial (up to bundle isomorphism), so without loss of generality
. A fibre bundle over a contractible space is trivial (up to bundle isomorphism), so without loss of generality 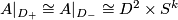 . We can now glue back the bundles via an automorphism of the fibre at every point on the boundary
. We can now glue back the bundles via an automorphism of the fibre at every point on the boundary 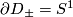 , varying continuously on the base i.e. a continuous map
, varying continuously on the base i.e. a continuous map 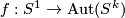 . In fact, a homotopic map
. In fact, a homotopic map 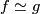 will produce an isomorphic bundle so we are interested in a class of
will produce an isomorphic bundle so we are interested in a class of ![\displaystyle [S^1,\text{Aut}(S^k)]=[S^1,SO(k+1)]=\Z_2](/images/math/7/3/2/732a442e4b85bf57179456bec11f5893.png)
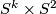 and so the other will be called the twisted bundle
and so the other will be called the twisted bundle 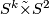 .
.Part 2
The sphere bundle of a 2-plane bundle is an
 -bundle, so the arguments from above carry through here as well. The sphere bundle of
-bundle, so the arguments from above carry through here as well. The sphere bundle of 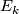 is given by the clutching construction above with the clutching map an element of
is given by the clutching construction above with the clutching map an element of ![\displaystyle [S^1,\text{Aut}(S^1)]=[S^1,SO(2)]=[S^1,S^1]=\Z,](/images/math/8/8/f/88fa8ca7fed5b22e654822734b447760.png)
 in
in  for surgery. We use the standard embedding of a sphere inside a larger sphere:
for surgery. We use the standard embedding of a sphere inside a larger sphere: 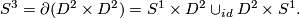
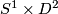 in the first factor where the framing is given by twisting the meridian around
in the first factor where the framing is given by twisting the meridian around  times as we pass around the
times as we pass around the  i.e. it is the element
i.e. it is the element ![k\in[S^1,\text{Aut}(D^2)]=\Z](/images/math/d/e/c/dececeb59e668c193bfcb7b912fae039.png) represented by a map
represented by a map 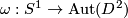 . Now do surgery. The effect is the gluing
. Now do surgery. The effect is the gluing 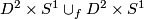
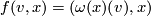 . This is now just the clutching construction as above.
. This is now just the clutching construction as above.Part 3
As  is nullhomotopically embedded, we may consider this inside a contractible disk, or in the second summand of
is nullhomotopically embedded, we may consider this inside a contractible disk, or in the second summand of 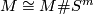 . Moreover we may embed it using the standard embedding
. Moreover we may embed it using the standard embedding 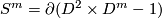 as above. Hence the result will be
as above. Hence the result will be 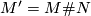 where
where  is either the trivial or twisted linear
is either the trivial or twisted linear 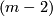 -sphere bundle over
-sphere bundle over  . As
. As  is spin, if
is spin, if  is the trivial bundle then the effect of surgery is also spin. However, if
is the trivial bundle then the effect of surgery is also spin. However, if  is twisted then
is twisted then 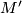 cannot be spin as connect sum results in direct sum of second Stiefel-Whitney classes and
cannot be spin as connect sum results in direct sum of second Stiefel-Whitney classes and 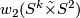 is non-vanishing. To see this consider that the bundle over
is non-vanishing. To see this consider that the bundle over  itself is not spin (that it is clutched by the non-trivial element of
itself is not spin (that it is clutched by the non-trivial element of 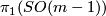 is more or less the definition of the obstruction to lifting to the spin group) and that this implies that the total space
is more or less the definition of the obstruction to lifting to the spin group) and that this implies that the total space 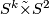 is also spin.
is also spin.
Now the hard part! Assume  is not spin, this means that there is a cocycle on which
is not spin, this means that there is a cocycle on which 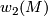 does not vanish.
does not vanish.
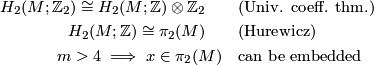
 on which
on which 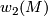 does not vanish and call this the weird sphere. Then this
does not vanish and call this the weird sphere. Then this  must have twisted normal bundle. Consider that for our untwisted surgery,
must have twisted normal bundle. Consider that for our untwisted surgery,  must initially bound a disk and we can extend the normal framing of
must initially bound a disk and we can extend the normal framing of  to the normal framing on
to the normal framing on 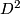 (which is necessarily trivial). For the twisted surgery,
(which is necessarily trivial). For the twisted surgery,  must have the other framing. Take the
must have the other framing. Take the 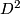 bounded by
bounded by  to be inside a hemisphere of the weird sphere. Now form an isotopy moving
to be inside a hemisphere of the weird sphere. Now form an isotopy moving  from one hemisphere to the other of the weird sphere. This must necessarily exchange the framing we have on
from one hemisphere to the other of the weird sphere. This must necessarily exchange the framing we have on  from trivial to twisted as the normal bundle of the weird sphere is twisted. However, the surgery at either end of an isotopy gives a diffeomorphic effect.
from trivial to twisted as the normal bundle of the weird sphere is twisted. However, the surgery at either end of an isotopy gives a diffeomorphic effect.To see this last part a different way, we may take a cylinder ![M\times [0,1]](/images/math/1/7/e/17ed67ecab55763a136c4659f8081368.png) . This induces a trivial isotopy of the embedded
. This induces a trivial isotopy of the embedded  . At some
. At some ![t\in[0,1]](/images/math/4/0/d/40de672f62756d608425bb0e58f1dfa1.png) , take a connect sum with the weird sphere and the isotopy
, take a connect sum with the weird sphere and the isotopy ![S^1\times[0,1]](/images/math/a/5/9/a5985bfdc2fa45d25755103ea33da323.png) . Now make the
. Now make the  slide along the tube and then over the weird sphere and down to the bottom of the tube as
slide along the tube and then over the weird sphere and down to the bottom of the tube as  increases from 0 to 1. This is not an isotopy but is now a concordance. However, within codimension
increases from 0 to 1. This is not an isotopy but is now a concordance. However, within codimension 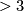 we can improve a concordance to an isotopy.
we can improve a concordance to an isotopy.
This does not cover the case 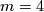 , I think it is still possible here but I don't have the solution.
, I think it is still possible here but I don't have the solution.