Talk:Smoothings of products (Ex)
From Manifold Atlas
(Difference between revisions)
(Created page with "<wikitex>; Let $\alpha \colon X \to BO$ and $\beta \colon Y \to BO$ be the given smooth structures. Recall the definition of $$ \Psi_\alpha \colon Conc(X) \to [X, PL/O]. $$ ...") |
m |
||
| Line 5: | Line 5: | ||
$$ \Psi_\alpha \colon Conc(X) \to [X, PL/O]. $$ | $$ \Psi_\alpha \colon Conc(X) \to [X, PL/O]. $$ | ||
Given a smooth structure $\xi \colon X \to BO$, consider $\Delta_X^* (\xi \oplus- \alpha) \colon X \to BO$. In the diagram | Given a smooth structure $\xi \colon X \to BO$, consider $\Delta_X^* (\xi \oplus- \alpha) \colon X \to BO$. In the diagram | ||
| − | $$\xymatrix{ | + | $$ |
| − | + | \xymatrix{ | |
| − | X\ar[r]_{\Delta_X^*(\xi \oplus -\alpha)}\ar[ur]^{\psi_\alpha(\xi)} & BO\ar[d] \\ | + | & PL/O\ar[d] \\ |
| − | & BPL } $$ | + | X\ar[r]_{\Delta_X^*(\xi \oplus -\alpha)}\ar[ur]^{\psi_\alpha(\xi)} & BO\ar[d]\\ |
| + | & BPL},$$ | ||
the lift $\psi_\alpha(\xi) $ (which is unique up to homotopy) results from the fact that the composition $X \xrightarrow{\Delta_X^*(\xi \oplus -\alpha)} BO \to BPL$ is nullhomotopic ($ \xi $ and $\alpha$ are lifts of the same PL structure). Then | the lift $\psi_\alpha(\xi) $ (which is unique up to homotopy) results from the fact that the composition $X \xrightarrow{\Delta_X^*(\xi \oplus -\alpha)} BO \to BPL$ is nullhomotopic ($ \xi $ and $\alpha$ are lifts of the same PL structure). Then | ||
$$ \Psi_\alpha(\xi) = [\psi_\alpha(\xi)].$$ | $$ \Psi_\alpha(\xi) = [\psi_\alpha(\xi)].$$ | ||
Latest revision as of 19:53, 29 August 2013
Let 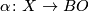 and
and 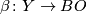 be the given smooth structures.
be the given smooth structures.
Recall the definition of
![\displaystyle \Psi_\alpha \colon Conc(X) \to [X, PL/O].](/images/math/9/9/f/99fd0f8f56817380209abf37322a5e34.png)
Given a smooth structure 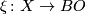 , consider
, consider 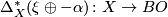 . In the diagram
. In the diagram
![\displaystyle \xymatrix{ & PL/O\ar[d] \\ X\ar[r]_{\Delta_X^*(\xi \oplus -\alpha)}\ar[ur]^{\psi_\alpha(\xi)} & BO\ar[d]\\ & BPL},](/images/math/2/0/3/203f472bc4aedb9058e3f9b566f01eaf.png)
the lift 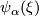 (which is unique up to homotopy) results from the fact that the composition
(which is unique up to homotopy) results from the fact that the composition 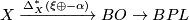 is nullhomotopic (
is nullhomotopic (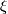 and
and 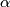 are lifts of the same PL structure). Then
are lifts of the same PL structure). Then
![\displaystyle \Psi_\alpha(\xi) = [\psi_\alpha(\xi)].](/images/math/6/6/d/66d5a67ca70ab5cd79c6677e94af46d5.png)
The PL homeomorphisms 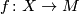 and
and 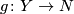 induce a smooth structure on
induce a smooth structure on 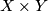 via the map
via the map
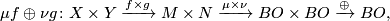
where 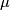 and
and  classify the stable tangent bundle of
classify the stable tangent bundle of  and
and 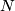 , respectively.
, respectively.
We now have
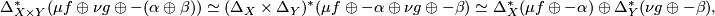
where we have used that  is homotopy associative and homotopy commutative.
is homotopy associative and homotopy commutative.
Since 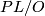 is the homotopy fibre of the infinite loop map
is the homotopy fibre of the infinite loop map 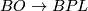 , a lift of this map is now given by
, a lift of this map is now given by 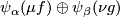 (
(  denoting now the induced
denoting now the induced 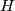 -space structure on
-space structure on 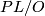 ).
).
Therefore, we get
![\displaystyle \Psi_{\alpha \times \beta}( f \times g) = \Psi_\alpha (f) \oplus \Psi_\beta(g) = [ X \times Y \xrightarrow{\psi_\alpha (\mu f) \times \psi_\beta(\nu g)} PL/O \times PL/O \xrightarrow{\oplus} PL/O ].](/images/math/7/a/e/7ae3cff6d1ecaa7a78d61440a88c4a60.png)