Talk:Reducible Poincaré Complexes (Ex)
From Manifold Atlas
Revision as of 18:00, 30 May 2012 by Andrzej Czarnecki (Talk | contribs)
1. Let's quickly prove the mentioned theorem of Wall. Assume that  is connected. The collection of top-dimensional
is connected. The collection of top-dimensional  -cells
-cells  is such that
is such that 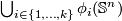 is connected - otherwise any two connected components would give two independent classes in
is connected - otherwise any two connected components would give two independent classes in 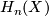 . Assume that
. Assume that  is pointed and that all attaching maps are pointed as well. We can take
is pointed and that all attaching maps are pointed as well. We can take 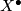 to be the
to be the  -skeleton of
-skeleton of  and the unique
and the unique  -cell to have the attaching map
-cell to have the attaching map
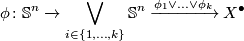
begginning with the pinching map.