Talk:Normal bordism - definitions (Ex)
(Difference between revisions)
| Line 17: | Line 17: | ||
\right\} | \right\} | ||
$$ | $$ | ||
| + | where we identify $(\xi_0,M_0,i_0,f_0,\overline{f_0})\sim(\xi_1,M_1,i_1,f_1,\overline{f_1})$ iff | ||
| + | |||
| + | 1) there exists $W$ compact manifold of dimension $n+1$ such that $\partial W=\partial_0W\amalg\partial_1W$ | ||
| + | |||
| + | 2) there exists an embedding $I$: $W\to\mathbb{R}^{n+k}\times[0,1]$ such that for $j=0,1$ we have | ||
| + | $I^{-1}(\mathbb{R}^{n+k}\times\{j\})=\partial_jW$ and $W$ meets $\mathbb{R}^{n+k}\times\{j\}$ transversally | ||
</wikitex> | </wikitex> | ||
Revision as of 10:47, 2 April 2012
Part 1
Let 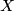 be a connected finite Poincare complex of dimension
be a connected finite Poincare complex of dimension 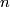 and let
and let 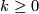 .
We define
.
We define
![\displaystyle \mathcal{N}_n(X,k):= \left\{ [\xi,M,i,f,\overline{f}] | \begin{array}{l} \xi\textrm{ vector bundle of rank }k\textrm{ over }X,\, M\textrm{ closed manifold of dimension }n,\, i:\,M\to\mathbb{R}^{n+k}\textrm{ embedding},\, (f,\overline{f}):\,\nu(M,i)\to\xi\textrm{ bundle map},\, f\textrm{ of degree }1 \end{array} \right\}](/images/math/3/8/9/38962ae773ef41b834b8be2c52e0655e.png)
where we identify 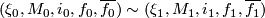 iff
iff
1) there exists 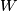 compact manifold of dimension
compact manifold of dimension 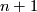 such that
such that 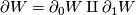
2) there exists an embedding 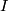 :
: ![W\to\mathbb{R}^{n+k}\times[0,1]](/images/math/a/b/1/ab18bc810bf5b65819b8394370060ae0.png) such that for
such that for 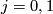 we have
we have
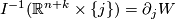 and
and 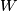 meets
meets 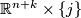 transversally
transversally