Talk:L2-Betti numbers for the universal covering of the circle (Ex)

Latest revision as of 05:54, 10 January 2019

I don't feel comfortable writing the solution here since I have seen $<wikitex>; I don't feel comfortable writing the solution here since I have seen $L^2$ before. But if you are stuck, here are possible suggestions, each an independent way to solve it: 0. You could just calculate the $L^2$ homology, it's very easy. 1. 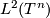$L^2(T^n)$ has nice behavior from a functional analytic perspective, and 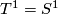$T^1 = S^1$. You can determine its group von Neumann algebra very explicitly. See Luck's book ''L2-invariants'', Example 1.4. 2. The fundamental group of $\mathbb Z$ is very nice and Slide 4 of [http://www.him.uni-bonn.de/lueck/data/Melbourne_IV_L2-invariants190110.pdf Luck's slides] has an applicable theorem. (Also Lemma 1.34 from his book.) 3. $L^2$ homology satisfies various homotopy-theoretic properties; see Theorem 1.35 in Luck's book. Then a solution that is both very stupid and very amusing is to use Lott-Luck, in Slide 5, with a 3-manifold with appropriate boundary. </wikitex>L^2$ before. But if you are stuck, here are possible suggestions, each an independent way to solve it:

0. You could just calculate the $L^2$ homology, it's very easy.

1. $L^2(T^n)$ has nice behavior from a functional analytic perspective, and $T^1 = S^1$. You can determine its group von Neumann algebra very explicitly. See Luck's book L2-invariants, Example 1.4.

2. The fundamental group of $\mathbb Z$ is very nice and Slide 4 of Luck's slides has an applicable theorem. (Also Lemma 1.34 from his book.)

3. $L^2$ homology satisfies various homotopy-theoretic properties; see Theorem 1.35 in Luck's book. Then a solution that is both very stupid and very amusing is to use Lott-Luck, in Slide 5, with a 3-manifold with appropriate boundary.