-
For starters the braid looks as follows:
Filling in the 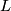 -groups (which were computed by Kervaire and Milnor), the homotopy groups of the orthogonal group (which are given by Bott periodicity), the framed bordism groups (which were shown to be the stable stems by Pontryagin and in low dimensions computed by Serre), and the
-groups (which were computed by Kervaire and Milnor), the homotopy groups of the orthogonal group (which are given by Bott periodicity), the framed bordism groups (which were shown to be the stable stems by Pontryagin and in low dimensions computed by Serre), and the 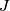 -homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
-homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
where we have used  to denote the map induced by the Kervaire invariant
to denote the map induced by the Kervaire invariant 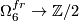 . Using that this is surjective (
. Using that this is surjective (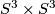 with its Lie-group framing has Kervaire-invariant
with its Lie-group framing has Kervaire-invariant 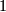 )
and the fact that the signature of an almost framed
)
and the fact that the signature of an almost framed 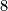 -manifold is divisible by
-manifold is divisible by  (and
(and  is actually the signature of ???), we obtain the following maps:
is actually the signature of ???), we obtain the following maps:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar@{^{(}->}[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr]^0 && \Z \ar[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^\cong \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]^0\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_8 \ar[dr] \ar^{28}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr]_\cong \ar@{^{(}->}[ur]^0 && \Omega^{alm}_6 \ar[dr] \ar[ur]^\cong && \Theta_{5}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_5 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]_0\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/9/0/7/9070dd1ce3e34b65b859bfa34ac00927.png)
$)
and the fact that the signature of an almost framed $-manifold is divisible by $ (and $ is actually the signature of ???), we obtain the following maps:
$$
\def\curv{1.5pc}
\xymatrix{
\Z/2 \ar@{^{(}->}[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr]^0 && \Z \ar[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar@{->>}[dr]\ar@/u\curv/[rr]&&
0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^\cong \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]^0\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \
& \Theta_{8}^{fr} \ar[dr] \ar[ur]^\cong
&& \Omega^{alm}_8 \ar[dr] \ar^{28}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur]
&& \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr]_\cong \ar@{^{(}->}[ur]^0
&& \Omega^{alm}_6 \ar[dr] \ar[ur]^\cong && \Theta_{5}^{fr} \ar[dr] \ar[ur]^\cong
&& \Omega^{alm}_5 \ar[dr] \ar[ur] & \
0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr]
&&\Z/240 \ar[ur]_0\ar@/d\curv/[rr] &&
0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr]
&&0 \ar[ur]\ar@/d\curv/[rr] && 0
}
$$
L-groups (which were computed by Kervaire and Milnor), the homotopy groups of the orthogonal group (which are given by Bott periodicity), the framed bordism groups (which were shown to be the stable stems by Pontryagin and in low dimensions computed by Serre), and the
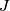
-homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
where we have used  to denote the map induced by the Kervaire invariant
to denote the map induced by the Kervaire invariant 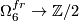 . Using that this is surjective (
. Using that this is surjective (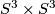 with its Lie-group framing has Kervaire-invariant
with its Lie-group framing has Kervaire-invariant 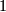 )
and the fact that the signature of an almost framed
)
and the fact that the signature of an almost framed 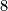 -manifold is divisible by
-manifold is divisible by  (and
(and  is actually the signature of ???), we obtain the following maps:
is actually the signature of ???), we obtain the following maps:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \pi_8(O) \ar[dr] \ar@/u\curv/^J[rr] && \Omega_8^{fr} \ar[dr] \ar@/u\curv/[rr] && L_8(\Z) \ar[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar[dr]\ar@/u\curv/[rr]&& \pi_6(O) \ar[dr] \ar@/u\curv/^J[rr] && \Omega_6^{fr} \ar[dr] \ar@/u\curv/[rr] && L_6(\Z) \ar[dr]\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& \pi_{4}(O) \ar[dr] \ar@/u\curv/^J[rr] && \Omega_{4}^{fr} \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_8 \ar[dr] \ar^s[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar_s[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_6 \ar[dr] \ar^s[ur] && \Theta_{5}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_5 \ar_s[dr] \ar[ur] && \Theta_{4}^{fr} \ar[dr] \ar[ur] & \\ L_9(\Z) \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \pi_7(O) \ar[ur] \ar@/d\curv/_J[rr] &&\Omega_7^{fr} \ar[ur]\ar@/d\curv/[rr] && L_7(\Z) \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && \pi_5(O) \ar[ur] \ar@/d\curv/_J[rr] &&\Omega_5^{fr} \ar[ur]\ar@/d\curv/[rr] && L_5(\Z) \ar[ur] \ar@/d\curv/[rr] && \Theta_{4} }](/images/math/2/9/5/295faa86dd0b821f62ab699b7a2a0494.png)
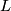 -groups (which were computed by Kervaire and Milnor), the homotopy groups of the orthogonal group (which are given by Bott periodicity), the framed bordism groups (which were shown to be the stable stems by Pontryagin and in low dimensions computed by Serre), and the
-groups (which were computed by Kervaire and Milnor), the homotopy groups of the orthogonal group (which are given by Bott periodicity), the framed bordism groups (which were shown to be the stable stems by Pontryagin and in low dimensions computed by Serre), and the 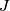 -homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
-homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr] && \Z \ar@{^{(}->}[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr] \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_8 \ar[dr] \ar^{sign}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_6 \ar[dr] \ar[ur] && \Theta_{5}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_5 \ar[dr] \ar[ur] && \Theta_{4}^{fr} \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_{4} }](/images/math/2/2/d/22df87b323a9b6da9382f7e37f5366ec.png)
 to denote the map induced by the Kervaire invariant
to denote the map induced by the Kervaire invariant 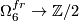 . Using that this is surjective (
. Using that this is surjective (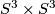 with its Lie-group framing has Kervaire-invariant
with its Lie-group framing has Kervaire-invariant 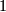 )
and the fact that the signature of an almost framed
)
and the fact that the signature of an almost framed 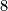 -manifold is divisible by
-manifold is divisible by  (and
(and  is actually the signature of ???), we obtain the following maps:
is actually the signature of ???), we obtain the following maps:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar@{^{(}->}[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr]^0 && \Z \ar[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^\cong \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]^0\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_8 \ar[dr] \ar^{28}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr]_\cong \ar@{^{(}->}[ur]^0 && \Omega^{alm}_6 \ar[dr] \ar[ur]^\cong && \Theta_{5}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_5 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]_0\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/9/0/7/9070dd1ce3e34b65b859bfa34ac00927.png)
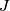 -homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
-homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr] && \Z \ar@{^{(}->}[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr] \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_8 \ar[dr] \ar^{sign}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_6 \ar[dr] \ar[ur] && \Theta_{5}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_5 \ar[dr] \ar[ur] && \Theta_{4}^{fr} \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_{4} }](/images/math/2/2/d/22df87b323a9b6da9382f7e37f5366ec.png)
 to denote the map induced by the Kervaire invariant
to denote the map induced by the Kervaire invariant 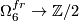 . Using that this is surjective (
. Using that this is surjective (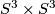 with its Lie-group framing has Kervaire-invariant
with its Lie-group framing has Kervaire-invariant 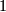 )
and the fact that the signature of an almost framed
)
and the fact that the signature of an almost framed 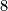 -manifold is divisible by
-manifold is divisible by  (and
(and  is actually the signature of ???), we obtain the following maps:
is actually the signature of ???), we obtain the following maps:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar@{^{(}->}[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr]^0 && \Z \ar[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^\cong \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]^0\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_8 \ar[dr] \ar^{28}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr]_\cong \ar@{^{(}->}[ur]^0 && \Omega^{alm}_6 \ar[dr] \ar[ur]^\cong && \Theta_{5}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_5 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]_0\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/9/0/7/9070dd1ce3e34b65b859bfa34ac00927.png)