Talk:K-groups of oriented surface groups (Ex)

First we look at the Atiyah-Hirzebruch spectral sequence. Recall that a closed orientable surface is either $S^2$$\newcommand{\Z}{\mathbb{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\F}{\mathbb{F}} \newcommand{\bZ}{\mathbb{Z}} \newcommand{\bR}{\mathbb{R}} \newcommand{\bC}{\mathbb{C}} \newcommand{\bH}{\mathbb{H}} \newcommand{\bQ}{\mathbb{Q}} \newcommand{\bF}{\mathbb{F}} \newcommand{\bN}{\mathbb{N}} \DeclareMathOperator\id{id} % identity map \DeclareMathOperator\Sq{Sq} % Steenrod squares \DeclareMathOperator\Homeo{Homeo} % group of homeomorphisms of a topoloical space \DeclareMathOperator\Diff{Diff} % group of diffeomorphisms of a smooth manifold \DeclareMathOperator\SDiff{SDiff} % diffeomorphism under some constraint \DeclareMathOperator\Hom{Hom} % homomrphism group \DeclareMathOperator\End{End} % endomorphism group \DeclareMathOperator\Aut{Aut} % automorphism group \DeclareMathOperator\Inn{Inn} % inner automorphisms \DeclareMathOperator\Out{Out} % outer automorphism group \DeclareMathOperator\vol{vol} % volume \newcommand{\GL}{\text{GL}} % general linear group \newcommand{\SL}{\text{SL}} % special linear group \newcommand{\SO}{\text{SO}} % special orthogonal group \newcommand{\O}{\text{O}} % orthogonal group \newcommand{\SU}{\text{SU}} % special unitary group \newcommand{\Spin}{\text{Spin}} % Spin group \newcommand{\RP}{\Rr\mathrm P} % real projective space \newcommand{\CP}{\Cc\mathrm P} % complex projective space \newcommand{\HP}{\Hh\mathrm P} % quaternionic projective space \newcommand{\Top}{\mathrm{Top}} % topological category \newcommand{\PL}{\mathrm{PL}} % piecewise linear category \newcommand{\Cat}{\mathrm{Cat}} % any category \newcommand{\KS}{\text{KS}} % Kirby-Siebenmann class \newcommand{\Hud}{\text{Hud}} % Hudson torus \newcommand{\Ker}{\text{Ker}} % Kernel \newcommand{\underbar}{\underline} %Classifying Spaces for Families of Subgroups \newcommand{\textup}{\text} \newcommand{\sp}{^}S^2$ or aspherical. Hence if $G$$G$ is not the trivial group, then the surface is itself a model for $BG$$BG$. 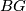Let us fix the genus $g$$g$ of the surface. Then the integral homology looks like

$\displaystyle H_*(BG;\Z) \cong \begin{cases} \Z & \text{ if } * \in \{0,2\}, \\ \Z^{2g} & \text{ if } * = 1, \\ 0 & \text{ else. }\end{cases}$ $$\displaystyle H_*(BG;\Z) \cong \begin{cases} \Z & \text{ if } * \in \{0,2\}, \\ \Z^{2g} & \text{ if } * = 1, \\ 0 & \text{ else. }\end{cases}$$

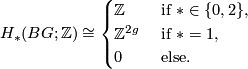
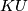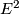Moreover since the coefficients of $KU$$KU$ are only $\Z$$\Z$ or $0$$0$ we see that all $E^2$$E^2$-terms of the spectral sequence are free abelian groups. By purely formal reasons there cannot be any non-trivial differential (the only possible ones have target the $y$$y$-axis of the spectral sequence, but since the coefficients in the AHSS always split off, these maps must have trivial image). 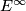Hence also the $E^\infty$$E^\infty$-terms of the spectral sequence are torsion free. In particular there are no extension problems to solve and we can read off the abutment to be

$\displaystyle K_0(BG) \cong \Z^2 \text{ and } K_1(BG) \cong \Z^{2g} .$ $$\displaystyle K_0(BG) \cong \Z^2 \text{ and } K_1(BG) \cong \Z^{2g} .$$

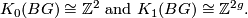
We want to remark that also for other homology theories there cannot occur non-trivial extensions when we want to compute the abutment from the 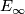$E_\infty$$E_\infty$-page. This follows from the following observation. The surface 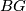$BG$$BG$ is given by a pushout

Tex syntax error

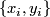where the attaching map is of the form $x_1 y_1 x_1^{-1} y_1^{-1} \dots x_g y_g x_g^{-1} y_g^{-1}$$x_1 y_1 x_1^{-1} y_1^{-1} \dots x_g y_g x_g^{-1} y_g^{-1}$ where the $1$$1$-cells are indexed over $\{x_i,y_i\}$$\{x_i,y_i\}$. In particular we see that suspending this map once, it becomes null-homotopic (higher homotopy groups are abelian). Hence, stably, the top cell of 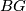$BG$$BG$ splits off and we can use the Mayer-Vietoris sequence to compute the homology of 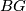$BG$$BG$ for any homology theory in terms of the coefficients.