Talk:K-group, zeroth (Ex)
Solution of 2
We will use the facts that every representation is uniquely determined by its character and that every representation decomposes as the direct sum of irreducible representations (this holds at least for representations of finite groups over algebraically closed fields). We begin by characterizing the class functions 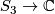 , i.e. the functions that only depend on the conjugacy classes. Notice that there are three conjugacy classes in
, i.e. the functions that only depend on the conjugacy classes. Notice that there are three conjugacy classes in 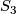 , one for each cycle type. Indeed, since each element of
, one for each cycle type. Indeed, since each element of 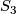 may be represented by a cycle of maximal length
may be represented by a cycle of maximal length  and the cycle length does not change under conjugation, we see that there are at least
and the cycle length does not change under conjugation, we see that there are at least  conjugacy classes. It is easy to check that all transpositions and the two
conjugacy classes. It is easy to check that all transpositions and the two  -cycles are conjugated to each other. Thus, a class function is uniquely determined by its values on, say,
-cycles are conjugated to each other. Thus, a class function is uniquely determined by its values on, say, 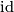 ,
, 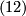 ,
, 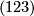 and, conversely, an element of
and, conversely, an element of 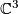 uniquely determines a class function. Consequently, the space of class functions is
uniquely determines a class function. Consequently, the space of class functions is  -dimensional, which is the same as saying that there are, up to isomorphism, three irreducible representations on
-dimensional, which is the same as saying that there are, up to isomorphism, three irreducible representations on 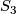 since the irreducible characters span the space of class functions.
since the irreducible characters span the space of class functions.
The first two are found quickly: Of course, the trivial representation 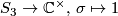 and the sign-representation
and the sign-representation 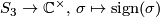 are irreducible (they are both one-dimensional!) and they cannot be isomorphic because their characters differ.
are irreducible (they are both one-dimensional!) and they cannot be isomorphic because their characters differ.
The natural representation of 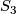 as permutation matrices on
as permutation matrices on 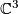 is not irreducible, as the hyperplane
is not irreducible, as the hyperplane 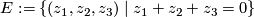 is invariant under permutation of coordinates. But the induced representation on
is invariant under permutation of coordinates. But the induced representation on  is irreducible: A one-dimensional subspace
is irreducible: A one-dimensional subspace 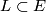 cannot be invariant under permutation of coordinates because if it was, it would be spanned by, say,
cannot be invariant under permutation of coordinates because if it was, it would be spanned by, say, 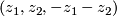 and then it would follow that
and then it would follow that 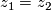 (because
(because  is invariant under
is invariant under 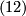 ) which implies
) which implies 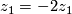 (because
(because  is invariant under
is invariant under 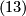 ) so that
) so that  would be spanned by zero, a contradiction (I would like to see a quicker argument here but could not come up with one.)
would be spanned by zero, a contradiction (I would like to see a quicker argument here but could not come up with one.)
Now we represent the three characters by elements of 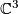 (i.e. their values on
(i.e. their values on 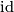 ,
, 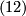 ,
, 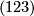 ): The trivial representation corresponds to
): The trivial representation corresponds to 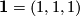 , the sign representation corresponds to
, the sign representation corresponds to 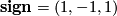 and the permutation representation corresponds to
and the permutation representation corresponds to 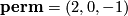 . Recalling that the multiplication in
. Recalling that the multiplication in 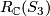 is given by the tensor product which corresponds to pointwise multiplication in the space of class funcions, i.e to componentwise multiplication on
is given by the tensor product which corresponds to pointwise multiplication in the space of class funcions, i.e to componentwise multiplication on 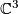 , we get the following multiplication table:
, we get the following multiplication table:
 |
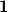 |
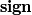 |
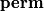
|
|---|---|---|---|
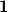
|
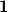
|
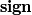
|
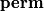
|
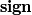
|
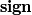
|
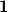
|
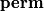
|
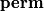
|
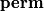
|
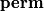
|
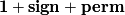
|
This shows that sending ![[\mathbf{sign}] \mapsto X](/images/math/8/c/2/8c28c225f90233cdcce02f32c036d452.png) and
and ![[\mathbf{perm}] \mapsto Y](/images/math/3/4/2/3426171d94fa3e5e4b48536e8f1b1547.png) induces a well-defined isomorphism
induces a well-defined isomorphism
![\displaystyle K_0(\C[S_3]) \simeq R_\C(S_3) \to \Z[X,Y] / (X^2 - 1, XY - Y, Y^2 - X - Y - 1).](/images/math/0/a/d/0adb6ddd26bd540aa433b7261039d5ef.png)