Talk:Chain duality III (Ex)
From Manifold Atlas
(Difference between revisions)
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | + | The most interesting part is to check equivariance, say for objects $M\in\mathbb A$. | |
Let $\varphi:TM\to M$ be an element of $M\otimes_{\mathbb A}M$. | Let $\varphi:TM\to M$ be an element of $M\otimes_{\mathbb A}M$. | ||
Latest revision as of 12:35, 1 June 2012
The most interesting part is to check equivariance, say for objects 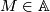 .
.
Let 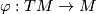 be an element of
be an element of 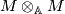 .
.
We have to check the equality of
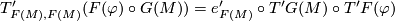
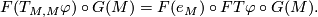
This follows from the commutative diagram
![\displaystyle \xymatrix{ T'F(M)\ar[r]^{T'F(\varphi)} \ar[d]_{G(M)} & T'FT(M) \ar[r]^{T'G(M)} \ar[d]_{G(TM)} & T'^2F(M) \ar[d]_{e'_{F(M)}}\\ FT(M)\ar[r]^{FT\varphi} & FT^2M\ar[r]^{Fe_M}& F(M) }](/images/math/2/b/5/2b5ea37128fc0cfef323cfd4e65d2a18.png)
as the first square commutes by naturality of  and the second one by definition of a
functor of categories with chain duality.
and the second one by definition of a
functor of categories with chain duality.