Talk:Borel Conjecture for the 2-torus (Ex)
(Difference between revisions)
| Line 1: | Line 1: | ||
| + | <wikitex>; | ||
The selfhomotopy equivalences of an Eilenberg-Mac Lane space of type $(G,n)$ generally have $\pi_0 = Out(G)$, detected by the action of fundamental groups, and $\pi_n = C(G)$, with all other homotopy groups vanishing. In particular, $\pi_0(hAut(T^2)) = Gl_2(\mathbb Z)$ is detected by the action on $H_1(T^2)$ and all we have to do is produce a homeomorphism that acts by a given matrix $A \in Gl_2(\mathbb Z)$. But via the identification $T^2 = \mathbb R^2/\mathbb Z^2$ the action of $A$ on $\mathbb R^2$ produces such an element. | The selfhomotopy equivalences of an Eilenberg-Mac Lane space of type $(G,n)$ generally have $\pi_0 = Out(G)$, detected by the action of fundamental groups, and $\pi_n = C(G)$, with all other homotopy groups vanishing. In particular, $\pi_0(hAut(T^2)) = Gl_2(\mathbb Z)$ is detected by the action on $H_1(T^2)$ and all we have to do is produce a homeomorphism that acts by a given matrix $A \in Gl_2(\mathbb Z)$. But via the identification $T^2 = \mathbb R^2/\mathbb Z^2$ the action of $A$ on $\mathbb R^2$ produces such an element. | ||
The same argument shows that the inclusion $Diff(T^n) \rightarrow hAut(T^n)$ splits on $pi_0$ In arbitrary dimensions. | The same argument shows that the inclusion $Diff(T^n) \rightarrow hAut(T^n)$ splits on $pi_0$ In arbitrary dimensions. | ||
| + | </wikitex> | ||
Revision as of 06:51, 10 January 2019
The selfhomotopy equivalences of an Eilenberg-Mac Lane space of type 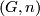 generally have
generally have 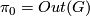 , detected by the action of fundamental groups, and
, detected by the action of fundamental groups, and 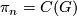 , with all other homotopy groups vanishing. In particular,
, with all other homotopy groups vanishing. In particular, 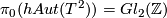 is detected by the action on
is detected by the action on 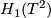 and all we have to do is produce a homeomorphism that acts by a given matrix
and all we have to do is produce a homeomorphism that acts by a given matrix 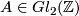 . But via the identification
. But via the identification 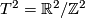 the action of
the action of  on
on 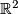 produces such an element.
produces such an element.
The same argument shows that the inclusion 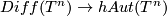 splits on
splits on 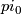 In arbitrary dimensions.
In arbitrary dimensions.