Talk:Borel Conjecture for the 2-torus (Ex)
(Created page with "<wikitex>; Suggestion: 1. Note that the dimensions must be equal. 2. Use the homotopy classification of surfaces, so both surfaces must be $T^2$. 3. Use the square model fo...") |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | + | The selfhomotopy equivalences of an Eilenberg-Mac Lane space of type $(G,n)$ generally have $\pi_0 = Out(G)$, detected by the action of fundamental groups, and $\pi_n = C(G)$, with all other homotopy groups vanishing. In particular, $\pi_0(hAut(T^2)) = Gl_2(\mathbb Z)$ is detected by the action on $H_1(T^2)$ and all we have to do is produce a homeomorphism that acts by a given matrix $A \in Gl_2(\mathbb Z)$. But via the identification $T^2 = \mathbb R^2/\mathbb Z^2$ the action of $A$ on $\mathbb R^2$ produces such an element. | |
| − | + | The same argument shows that the inclusion $Diff(T^n) \rightarrow hAut(T^n)$ splits on $pi_0$ In arbitrary dimensions. | |
| − | |||
| − | + | Note: as described by a (now erased) suggestion, there is a more elementary method. You can treat the map as a periodic map $\mathbb R^2 \to \mathbb R^2$ sending every lattice point to itself. This is because the image of the origin's generators also generate the target's homology. This map of $\mathbb R^2$ can be homotoped to the identity map linearly, producing a diffeomorphism. This also works for any $T^n$, as the above proof does. | |
</wikitex> | </wikitex> | ||
Latest revision as of 08:24, 10 January 2019
The selfhomotopy equivalences of an Eilenberg-Mac Lane space of type 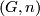 generally have
generally have 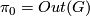 , detected by the action of fundamental groups, and
, detected by the action of fundamental groups, and 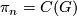 , with all other homotopy groups vanishing. In particular,
, with all other homotopy groups vanishing. In particular, 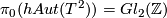 is detected by the action on
is detected by the action on 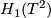 and all we have to do is produce a homeomorphism that acts by a given matrix
and all we have to do is produce a homeomorphism that acts by a given matrix 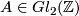 . But via the identification
. But via the identification 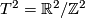 the action of
the action of  on
on 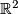 produces such an element.
produces such an element.
The same argument shows that the inclusion 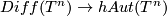 splits on
splits on 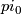 In arbitrary dimensions.
In arbitrary dimensions.
Note: as described by a (now erased) suggestion, there is a more elementary method. You can treat the map as a periodic map 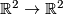 sending every lattice point to itself. This is because the image of the origin's generators also generate the target's homology. This map of
sending every lattice point to itself. This is because the image of the origin's generators also generate the target's homology. This map of 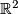 can be homotoped to the identity map linearly, producing a diffeomorphism. This also works for any
can be homotoped to the identity map linearly, producing a diffeomorphism. This also works for any 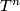 , as the above proof does.
, as the above proof does.