Surgery obstruction, signature (Ex)
(Difference between revisions)
(Created page with "<wikitex>; ... </wikitex> == References == {{#RefList:}} Category:Exercises Category:Exercises without solution") |
|||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | ... | + | '''1)''' Let $(\overline{f},f):M^{2n} \to X$ be an $n$-connected degree one normal map. Let $(K_n(M),\lambda, \mu)$ be the associated kernel form. Prove that signature satisfies the relation $$\mathrm{sign}(K_n(M),\lambda) = \mathrm{sign}(H_n(M),\lambda_M) - \mathrm{sign}(H_n(X),\lambda_X).$$ |
| + | |||
| + | '''2)''' Prove that if $\mathrm{sign}(K_n(M),\lambda)=0 $ then we can find a Lagrangian with respect to $\lambda$. (This is proven in \cite{Milnor1961|Lemma 8 and 9 of Milnor1961} | ||
| + | |||
| + | You may assume the following lemma: | ||
| + | {{beginthm|Lemma|\cite{Milnor1961|Lemma 8}} | ||
| + | A quadratic form $\varphi$ with integer coefficients and determinant $\pm 1$ has a non-trivial zero if and only if it is indefinite. | ||
| + | {{endthm}} | ||
| + | |||
</wikitex> | </wikitex> | ||
== References == | == References == | ||
Revision as of 21:32, 25 August 2013
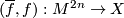 be an
be an 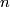 -connected degree one normal map. Let
-connected degree one normal map. Let 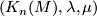 be the associated kernel form. Prove that signature satisfies the relation
be the associated kernel form. Prove that signature satisfies the relation 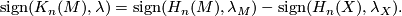
2) Prove that if 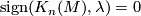 then we can find a Lagrangian with respect to
then we can find a Lagrangian with respect to 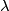 . (This is proven in [Milnor1961, Lemma 8 and 9 of Milnor1961]
. (This is proven in [Milnor1961, Lemma 8 and 9 of Milnor1961]
You may assume the following lemma:
{{beginthm|Lemma|[Milnor1961, Lemma 8]}
A quadratic form 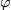 with integer coefficients and determinant
with integer coefficients and determinant 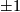 has a non-trivial zero if and only if it is indefinite.
</div>
has a non-trivial zero if and only if it is indefinite.
</div>
References
- [Milnor1961] J. Milnor, A procedure for killing homotopy groups of differentiable manifolds, Proc. Sympos. Pure Math, Vol. III (1961), 39–55. MR0130696 (24 #A556) Zbl 0118.18601