Surgery obstruction, Arf-invariant (Ex)
From Manifold Atlas
(Difference between revisions)
(Created page with "<wikitex>; ... </wikitex> == References == {{#RefList:}} Category:Exercises Category:Exercises without solution") |
|||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | ... | + | Let $(K,\lambda,\mu)$ be a $(-1)$-symmetric unimodular quadratic form over $\Z$ so that $(K,\lambda)\cong H_{-1}(\Z^r)$ with canonical basis $\{e_1,\ldots, e_r,f_1,\ldots, f_r\}$. Recall that the quadratic refinement $\mu: K \to \Z_2$ is a function such that for all $x,y\in K$, $$\mu(x+y) = \mu(x)+\mu(y) + \lambda(x,y)\quad (\mathrm{mod}\;2).$$ Define the '''Arf invariant''' of $(K,\lambda,\mu)$ by $$A(K,\lambda,\mu) := \sum_{i=1}^r\mu(e_i)\mu(f_i) \in \Z_2.$$ Prove that the Arf invariant is well-defined and defines an isomorphism $$A:L_2(\Z)\cong \Z_2.$$ |
| + | |||
| + | '''Hint:''' Start by classifying quadratic forms on $\Z^2$, use induction and also count the size of the sets $\mu^{-1}(0)$ and $\mu^{-1}(1)$. | ||
</wikitex> | </wikitex> | ||
== References == | == References == | ||
Latest revision as of 21:18, 25 August 2013
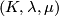 be a
be a 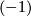 -symmetric unimodular quadratic form over
-symmetric unimodular quadratic form over  so that
so that 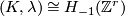 with canonical basis
with canonical basis 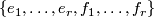 . Recall that the quadratic refinement
. Recall that the quadratic refinement 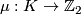 is a function such that for all
is a function such that for all 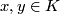 ,
, 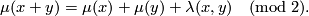
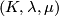 by
by 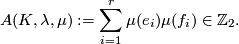
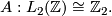
Hint: Start by classifying quadratic forms on 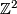 , use induction and also count the size of the sets
, use induction and also count the size of the sets 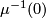 and
and 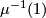 .
.