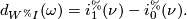Structured chain complexes III (Ex)
From Manifold Atlas
Revision as of 12:46, 30 July 2013 by Diarmuid Crowley (Talk | contribs)
Let 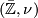 be the
be the  -dimensional symmetric complex where
-dimensional symmetric complex where
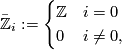
and the symmetric structure is given by
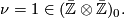
Let  be the cellular chain complex of the unit interval and let
be the cellular chain complex of the unit interval and let 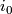 ,
, 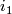 be the inclusions of the two ends. Find a
be the inclusions of the two ends. Find a  -dimensional chain
-dimensional chain 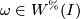 such that
such that
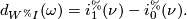
[edit] References
$-dimensional symmetric complex where $$ \bar \Zz_i := \begin{cases} \Zz & i = 0 \ 0 & i \neq 0, \end{cases} $$ and the symmetric structure is given by $$ \nu = 1 \in (\bar \Zz \otimes \bar \Zz)_0. $$ Let $I$ be the cellular chain complex of the unit interval and let $i_0$, $i_1$ be the inclusions of the two ends. Find a (\bar \Zz,\nu) be the -dimensional symmetric complex where
-dimensional symmetric complex where
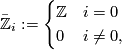
and the symmetric structure is given by
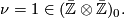
Let  be the cellular chain complex of the unit interval and let
be the cellular chain complex of the unit interval and let 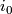 ,
, 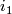 be the inclusions of the two ends. Find a
be the inclusions of the two ends. Find a  -dimensional chain
-dimensional chain 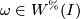 such that
such that
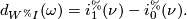
[edit] References
$-dimensional chain $\omega \in W^{\%}(I)$ such that $$ d_{W^{\%}{I}} (\omega) = i_1^{\%} (\nu) - i_0^{\%} (\nu). $$ == References== {{#RefList:}} [[Category:Exercises]] [[Category:Exercises without solution]](\bar \Zz,\nu) be the -dimensional symmetric complex where
-dimensional symmetric complex where
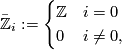
and the symmetric structure is given by
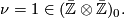
Let  be the cellular chain complex of the unit interval and let
be the cellular chain complex of the unit interval and let 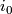 ,
, 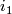 be the inclusions of the two ends. Find a
be the inclusions of the two ends. Find a  -dimensional chain
-dimensional chain 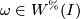 such that
such that