String bordism
Contents |
1 Introduction
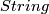 -bordism or
-bordism or 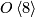 -bordism is a special case of a B-bordism. It comes from the tower of fibrations
-bordism is a special case of a B-bordism. It comes from the tower of fibrations
![\displaystyle \xymatrix{BO\left< 8 \right>\ar[d] & \\ BSpin \ar[d]\ar[r]^{p_1/2}&K({\mathbb Z},4) \\ BSO\ar[d]\ar[r]^{w_2}& K({\mathbb Z}/2,2) \\ BO\ar[r]^{w_1}& K({\mathbb Z}/2,1) }](/images/math/9/3/b/93b668e377b32aa99eb080e4db78b413.png)
In each step the lowest homotopy group is killed by the map into the Eilenberg-MacLane spaces. In particular, 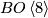 is the homotopy fibre of the map from
is the homotopy fibre of the map from 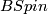 given by half of the first Pontryagin class. The name
given by half of the first Pontryagin class. The name 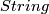 -group is due to Haynes Miller and will be explained below. There are various models for the String group.
-group is due to Haynes Miller and will be explained below. There are various models for the String group.
2 Additive structure
The additive structure of the bordism groups is not fully determined yet. Clearly, since 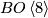 is 7-connected the first 6 bordism groups coincide with the framed bordism groups. It is known that only 2 and 3 torsion appears (see [Giambalvo1971] also for the first 16 bordism groups.)
is 7-connected the first 6 bordism groups coincide with the framed bordism groups. It is known that only 2 and 3 torsion appears (see [Giambalvo1971] also for the first 16 bordism groups.)
3 The Witten genus
At the end of the 80s Ed Witten were studying the  -equivariant index of the Dirac operator on a loop space of a
-equivariant index of the Dirac operator on a loop space of a  -dimensional manifold. For compact manifolds a Dirac operator exists if the manifold is Spin. For the loop space
-dimensional manifold. For compact manifolds a Dirac operator exists if the manifold is Spin. For the loop space 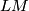 this would mean that
this would mean that  is
is 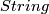 . Witten carried the Atiyah-Segal formula for the index over to this infinite dimensional setting and obtained an integral modular form of weight
. Witten carried the Atiyah-Segal formula for the index over to this infinite dimensional setting and obtained an integral modular form of weight  . Nowadays this is called the Witten genus (see [Segal1987].)
. Nowadays this is called the Witten genus (see [Segal1987].)
4 Characteristic numbers
The Witten genus can be refined to a map of structured ring spectra
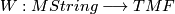
from the Thom spectrum of String bordism to the spectrum 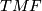 of topological modular forms. This spectrum was developed by Mike Hopkins (see [Hopkins2002].) It is supposed to play the same role for
of topological modular forms. This spectrum was developed by Mike Hopkins (see [Hopkins2002].) It is supposed to play the same role for 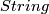 -bordism as
-bordism as 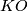 -theory does for
-theory does for  -bordism. Its coefficients localized away from 2 and 3 are given by the integral modular forms. The map
-bordism. Its coefficients localized away from 2 and 3 are given by the integral modular forms. The map  gives characteristic numbers which together with
gives characteristic numbers which together with 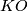 and Stiefel-Whitney numbers are conjectured to determine the
and Stiefel-Whitney numbers are conjectured to determine the 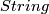 bordism class. Moreover,
bordism class. Moreover, 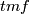 is supposed to be a direct summand of
is supposed to be a direct summand of 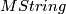 as the orientation map
as the orientation map  is shown to be surjective in homotopy (see [HopkinsMahowald2002].)
is shown to be surjective in homotopy (see [HopkinsMahowald2002].)
5 References
- [Giambalvo1971] V. Giambalvo, On
 -cobordism, Illinois J. Math. 15 (1971), 533–541. MR0287553 (44 #4757) Zbl 0221.57019
-cobordism, Illinois J. Math. 15 (1971), 533–541. MR0287553 (44 #4757) Zbl 0221.57019
- [Hopkins2002] M. J. Hopkins, Algebraic topology and modular forms, (2002), 291–317. MR1989190 (2004g:11032) Zbl 1031.55007
- [HopkinsMahowald2002] Template:HopkinsMahowald2002
- [Segal1987] Template:Segal1987
|
This page has not been refereed. The information given here might be incomplete or provisional. |