Splitting invariants (Ex)
From Manifold Atlas
(Difference between revisions)
m |
m |
||
| Line 9: | Line 9: | ||
[\mathbb{C}P^k, G/PL] \to L_{2k}(\mathbb{Z})$$ splits the above sequence for $k>2$. Additionally $[\mathbb{C}P^2,G/PL] \equiv \mathbb{Z}$ and the isomorphism is given by the surgery obstruction map. | [\mathbb{C}P^k, G/PL] \to L_{2k}(\mathbb{Z})$$ splits the above sequence for $k>2$. Additionally $[\mathbb{C}P^2,G/PL] \equiv \mathbb{Z}$ and the isomorphism is given by the surgery obstruction map. | ||
</wikitex> | </wikitex> | ||
| − | == References == | + | <!-- == References == |
| − | {{#RefList:}} | + | {{#RefList:}} --> |
[[Category:Exercises]] | [[Category:Exercises]] | ||
| + | [[Category:Exercises without solution]] | ||
Latest revision as of 15:00, 1 April 2012
Prove that two maps 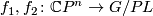 are
homotopic iff their splitting invariants agree for
are
homotopic iff their splitting invariants agree for 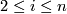 .
.
Use the exact sequence
![\displaystyle L_{2k}(\mathbb{Z}) \to [\mathbb{C}P^k,G/PL] \to [\mathbb{C}P^{k-1},G/PL] \to 0](/images/math/6/a/9/6a91b8ae34455f5fcf5e4d3774192247.png)
![\displaystyle \theta \colon [\mathbb{C}P^k, G/PL] \to L_{2k}(\mathbb{Z})](/images/math/0/1/6/01613f37724925f8fa94f2ff1958dd3e.png)
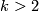 . Additionally
. Additionally ![[\mathbb{C}P^2,G/PL] \equiv \mathbb{Z}](/images/math/1/0/7/1076b8a5647c10603095ed9d952f7938.png) and the isomorphism is given by the surgery obstruction map.
and the isomorphism is given by the surgery obstruction map.