Sphere bundles and spin (Ex)
(Difference between revisions)
m |
m |
||
| Line 3: | Line 3: | ||
* Let $E_k\to S^2$ be the complex plane bundle with Euler number $k$. Explain how to obtain the total space of the sphere-bundle $S(E_k)$ via surgery on $S^3$. | * Let $E_k\to S^2$ be the complex plane bundle with Euler number $k$. Explain how to obtain the total space of the sphere-bundle $S(E_k)$ via surgery on $S^3$. | ||
| − | For $m\geq 4$ and $M$ a smooth closed manifold, let $S^1\hookrightarrow M^m$ be a nullhomotopic embedding. For $M$ spin, show that | + | For $m\geq 4$ and $M$ a smooth closed manifold, let $S^1\hookrightarrow M^m$ be a nullhomotopic embedding. For $M$ spin, show that there is more than one possible diffeormorphism type for the outcome of a surgery on this embedding. |
Now suppose $M$ is simply connected. For $M$ not spin, show that the outcome of a surgery on this embedding ''is'' uniquely determined up to diffeomorphism (difficult!). | Now suppose $M$ is simply connected. For $M$ not spin, show that the outcome of a surgery on this embedding ''is'' uniquely determined up to diffeomorphism (difficult!). | ||
Revision as of 23:04, 26 March 2012
- For
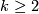 , determine the number of distinct linear
, determine the number of distinct linear 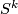 -bundles over
-bundles over  .
.
- Let
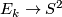 be the complex plane bundle with Euler number
be the complex plane bundle with Euler number  . Explain how to obtain the total space of the sphere-bundle
. Explain how to obtain the total space of the sphere-bundle 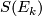 via surgery on
via surgery on  .
.
For 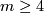 and
and  a smooth closed manifold, let
a smooth closed manifold, let 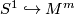 be a nullhomotopic embedding. For
be a nullhomotopic embedding. For  spin, show that there is more than one possible diffeormorphism type for the outcome of a surgery on this embedding.
spin, show that there is more than one possible diffeormorphism type for the outcome of a surgery on this embedding.
Now suppose  is simply connected. For
is simply connected. For  not spin, show that the outcome of a surgery on this embedding is uniquely determined up to diffeomorphism (difficult!).
not spin, show that the outcome of a surgery on this embedding is uniquely determined up to diffeomorphism (difficult!).