Some calculations involving configuration spaces of distinct points
m (→Introduction) |
m (→Construction and examples) |
||
| Line 37: | Line 37: | ||
$$ | $$ | ||
<!-- The Haefliger-Wu invariant and the Gauss map are analogously defined for $N_0$; we will denote them by $\alpha_0$ in this case.--> | <!-- The Haefliger-Wu invariant and the Gauss map are analogously defined for $N_0$; we will denote them by $\alpha_0$ in this case.--> | ||
| + | {{beginthm|Theorem}} | ||
| + | The Haefliger-Wu invariant $\alpha:\mathrm{Emb}^m N\to\pi^{m-1}_{\mathrm{eq}}( \widetilde N)$ is one-to-one for $2m\ge 3n+4$. | ||
{{endthm}} | {{endthm}} | ||
</wikitex> | </wikitex> | ||
Revision as of 14:02, 2 April 2020
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
‘The complement of the diagonal’ and ‘the Gauss map’ ideas play a greatrole in different branches of mathematics [Gl68, Va92]. The Haefliger-Wu invariant is amanifestation of these ideas in the theory of embeddings. The complement to the diagonalidea originated from two celebrated theorems: the Lefschetz Fixed Point Theorem andthe Borsuk-Ulam Antipodes Theorem
2 Construction and examples
For a manifold  ,
, 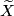 denotes the deleted product of
denotes the deleted product of  , i.e.
, i.e. 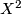 minus an open tubular neighborhood of the diagonal. It is a manifold with boundary and has the standard free involution.
minus an open tubular neighborhood of the diagonal. It is a manifold with boundary and has the standard free involution.
Definition 2.1.[of the Haefliger-Wu invariant  ]
]
The Haefliger-Wu invariant
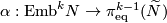 is induced by the Gauss map, also denoted by
is induced by the Gauss map, also denoted by  .
The Gauss map assigns to an individual embedding
.
The Gauss map assigns to an individual embedding 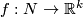 an equivariant map
an equivariant map 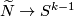 defined by the formula
defined by the formula
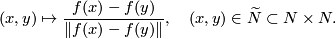
Theorem 2.2.
The Haefliger-Wu invariant 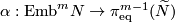 is one-to-one for
is one-to-one for  .
.
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...