Sandbox
|
The sandbox is the page where you can experiment with the wiki syntax. Feel free to write nonsense or clear the page whenever you want. |
- For the more general case where
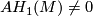 , see 6-manifolds: 1-connected.
, see 6-manifolds: 1-connected.
- For the more general case where
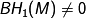 , see 6-manifolds: 1-connected.
, see 6-manifolds: 1-connected.
- For the more general case where
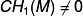 , see 6-manifolds: 1-connected.
, see 6-manifolds: 1-connected.
- For the more general case where
 , see 6-manifolds: 1-connected.
, see 6-manifolds: 1-connected.
- For the more general case where
 , see 6-manifolds: 1-connected.
, see 6-manifolds: 1-connected.
Contents |
1 Introduction
 Let
Let  be the set of diffeomorphism classes of closed smooth simply-connected 2-connected 6-manifolds
be the set of diffeomorphism classes of closed smooth simply-connected 2-connected 6-manifolds  .
.
The classification  was one of Smale's first applications of the h-cobordism theorem [Smale1962a, Corollary 1.3]. The classification, as for oriented surfaces is strikingly simple: every 2-connected 6-manifold
was one of Smale's first applications of the h-cobordism theorem [Smale1962a, Corollary 1.3]. The classification, as for oriented surfaces is strikingly simple: every 2-connected 6-manifold  is diffeomorphic to a connected-sum
is diffeomorphic to a connected-sum
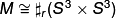
where by definition 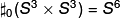 and in general
and in general  is determined by the formula for the Euler characteristic of
is determined by the formula for the Euler characteristic of 
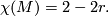
- For the more general case where
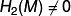 , see 6-manifolds: 1-connected.
, see 6-manifolds: 1-connected.
Construction and examples 
The following gives a complete list of 2-connected 6-manifolds up to diffeomorphism:
-
 , the standard 6-sphere.
, the standard 6-sphere.
-
 , the
, the  -fold connected sum of
-fold connected sum of 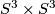 .
.
2 Invariants
Suppose that  is diffeomorphic to
is diffeomorphic to  then:
then:
-
 ,
,
- the third Betti-number of
 is given by
is given by 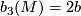 ,
,
- the Euler characteristic of
 is given by
is given by  ,
,
- the intersection form of
 is isomorphic to the sum of b-copies of
is isomorphic to the sum of b-copies of  , the standard skew-symmetric hyperbolic form on
, the standard skew-symmetric hyperbolic form on 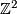 .
.
3 Classification
Recall that the following theorem was stated in other words in the introduction:
Theorem 4.1 [Smale1962a, Corolary 1.3]. The semi-group of 2-connected 6-manifolds is generated by $S^3 \times S^3$.
Hence if $\Nn$ denotes the natural numbers we obtain a bijection $$ \mathcal{M}_6(0)\equiv \Nn,Diarmuid Crowley[M] \mapsto \frac{1}{2}b_3(M).$$
4 Further discussion
4.1 Topological 2-connected 6-manifolds
Let $\mathcal{M}^{\Top}_6(e)$ be the set of homeomorphism classes of topological 2-connected 6-manifolds.
Theorem 5.1. Every topological 2-connected 6-manifold admits a smooth structure which is unique up to diffoemorphism. That is, there is a bijection $$ \mathcal{M}_6(e) \rightarrow \mathcal{M}^{\Top}_6(e).$$
Proof. For any such manifold $M$ we have $H^4(M; \Zz/2) \cong 0$ and so $M$ is smoothable (see 6-manifolds: 1-connected). Any two homeomorphic manifolds have the same Euler Characteristic and so by Theorem 4.1 are diffeomorphic.

4.2 Mapping class groups
... </wikitex>
5 References
- [Smale1962a] S. Smale, On the structure of manifolds, Amer. J. Math. 84 (1962), 387–399. MR0153022 (27 #2991) Zbl 0109.41103