Sandbox
m |
m |
||
| (26 intermediate revisions by 2 users not shown) | |||
| Line 12: | Line 12: | ||
}} --> | }} --> | ||
| − | + | <stepsectioncounter/> | |
| − | < | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | == File Creation Practice == | |
| − | + | [[Media:New_submission.pdf|Click here to access the pdf file]]. | |
| − | + | ||
| − | + | ||
| − | + | == Testing equation numbering == | |
| − | + | <wikitex>; | |
| − | + | \begin{equation} \label{eq:1} A = B \end{equation} | |
| + | Here is a reference to equation \ref{eq:1} | ||
| + | </wikitex> | ||
| + | == Still testing equation numbering == | ||
| + | <wikitex>; | ||
| + | \begin{equation}\label{test} C = D \end{equation} | ||
| + | \ref{test} | ||
</wikitex> | </wikitex> | ||
| − | == | + | == Lists== |
<wikitex>; | <wikitex>; | ||
| + | <ol style="list-tsyle-type:lower-roman> | ||
| + | <li>Frog</li> | ||
| + | </ol> | ||
| − | {{beginthm|Theorem| | + | $$ A \xrightarrow{f} B$$ |
| + | |||
| + | $--$ | ||
| + | </wikitex> | ||
| + | {{beginthm|Theorem|\cite{Penrose&Whitehead&Zeeman1961}}}\label{thm:2.1} | ||
For every compact $m$--dimensional PL-manifold $M$ there exists a PL--embedding $ M \hookrightarrow \R^{2m}$. | For every compact $m$--dimensional PL-manifold $M$ there exists a PL--embedding $ M \hookrightarrow \R^{2m}$. | ||
{{endthm}} | {{endthm}} | ||
| − | {{ | + | {{beginrem|Remark}} |
For a good exposition of Theorem \ref{thm:2.1} see also \cite{Rourke&Sanderson1972a|p. 63}. | For a good exposition of Theorem \ref{thm:2.1} see also \cite{Rourke&Sanderson1972a|p. 63}. | ||
| − | {{ | + | {{endrem}} |
{{beginthm|Theorem|\cite{Whitney1944}}}\label{thm:2.2} | {{beginthm|Theorem|\cite{Whitney1944}}}\label{thm:2.2} | ||
| Line 45: | Line 51: | ||
{{endthm}} | {{endthm}} | ||
| − | {{beginrem|Remark | + | {{beginrem|Remark}} |
For a more modern exposition see also \cite{Adachi1993|p. 67ff}. | For a more modern exposition see also \cite{Adachi1993|p. 67ff}. | ||
{{endrem}} | {{endrem}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\begin{theorem} \label{thm:1} | \begin{theorem} \label{thm:1} | ||
| Line 216: | Line 207: | ||
== Section == | == Section == | ||
<wikitex>; | <wikitex>; | ||
| + | |||
| + | '''$\textup{CW}_0$''' | ||
An [[map-eds:Manifold Atlas:Projects in the Atlas|inter-Wiki link]]. | An [[map-eds:Manifold Atlas:Projects in the Atlas|inter-Wiki link]]. | ||
| Line 221: | Line 214: | ||
Another <ref> Test1 </ref> [[map-eds:Manifold Atlas:Projects in the Atlas|inter-Wiki link]]. | Another <ref> Test1 </ref> [[map-eds:Manifold Atlas:Projects in the Atlas|inter-Wiki link]]. | ||
| − | |||
dfa<ref>Test2</ref> | dfa<ref>Test2</ref> | ||
| + | |||
| + | </wikitex> | ||
==Footnotes== | ==Footnotes== | ||
<references/> | <references/> | ||
| + | ==References== | ||
| + | {{#RefList:}} | ||
Latest revision as of 08:31, 15 October 2019
|
The sandbox is the page where you can experiment with the wiki syntax. Feel free to write nonsense or clear the page whenever you want. |
Contents |
[edit] 1 File Creation Practice
Click here to access the pdf file.
[edit] 2 Testing equation numbering
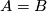
Here is a reference to equation 1
[edit] 3 Still testing equation numbering
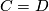
[edit] 4 Lists
- Frog
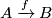

Theorem 5.1 [Penrose&Whitehead&Zeeman1961]. For every compact $m$--dimensional PL-manifold $M$ there exists a PL--embedding $ M \hookrightarrow \R^{2m}$.
Remark 5.2. For a good exposition of Theorem 5.1 see also [Rourke&Sanderson1972a, p. 63].
Theorem 5.3 [Whitney1944]. For every closed m--dimensional $C^{\infty}$--manifold $M$ there exists a $C^{\infty}$--embedding $M \hookrightarrow \R^{2m}$.
Remark 5.4. For a more modern exposition see also [Adachi1993, p. 67ff].
Theorem 5.5. We have $f \colon X \to Y$
Reference 5.5
By Theorem
{{#addlabel: test}}
Theorem 5.6. Frog
3 \ref{eqtest}
Here is some text leading up to an equation
5.7. $$ A = B $$
Here is some more text after the equation to see how it looks.
Here is some text leading up to an equation $$ A = B $$ Here is some more text after the equation to see how it looks.
4k 8 12 16 20 24 28 32 order bP4k 22.7 25.31 26.127 29.511 210.2047.691 213.8191 214.16384.3617
k 1 2 3 4 5 6 7 8 Bk 1/6 1/30 1/42 1/30 5/66 691/2730 7/6 3617/510
Dim n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 order Θn 1 1 1 1 1 1 28 2 8 6 992 1 3 2 16256 2 16 16 523264 24 bPn+1 1 1 1 1 1 1 28 1 2 1 992 1 1 1 8128 1 2 1 261632 1 Θn/bPn+1 1 1 1 1 1 1 1 2 2×2 6 1 1 3 2 2 2 2×2×2 8×2 2 24 πnS/J 1 2 1 1 1 2 1 2 2×2 6 1 1 3 2×2 2 2 2×2×2 8×2 2 24 index - 2 - - - 2 - - - - - - - 2 - - - - - -
$$ f \colon X \to Y $$
Extension DPL (warning): current configuration allows execution of DPL code from protected pages only.
Just a fest $f \colon A \to B$.
$\Q$
a theorem 5.8.
$\text{Spin}$
by theorem 5.8
- Amsterdam
- Rotterdam
- The Hague
[Mess1990]
$\left( \begin{array}{ll} \alpha & \beta \\ \gamma & \delta \end{array} \right)$
$f = T$
$ f : X \to Y$
$$ f : X \to Y $$
$\Ker$
$\mathscr{A}$ $\mathscr{B}$
bold italic emphasis
</wikitex>
[edit] 5 Tests
[Ranicki1981] [Milnor1956] [Milnor1956, Theorem 1] [Milnor1956] [Milnor1956, Theorem 1] Frog
Proof.

[edit] 6 Section
[edit] 6.1 Subsection
Refert to subsection 7.1
Theorem 7.1. test
Refer to theorem 7.1
[edit] 7 Section
An inter-Wiki link.
Another [1]; inter-Wiki link.
dfa[2]
[edit] 8 Footnotes
[edit] 9 References
- [Adachi1993] M. Adachi, Embeddings and immersions, Translated from the Japanese by Kiki Hudson. Translations of Mathematical Monographs, 124. Providence, RI: American Mathematical Society (AMS), 1993. MR1225100 (95a:57039) Zbl 0810.57001
- [Mess1990] G. Mess, Examples of Poincaré duality groups, Proc. Amer. Math. Soc. 110 (1990), no.4, 1145–1146. MR1019274 (91c:20075) Zbl 0709.57025
- [Milnor1956] J. Milnor, On manifolds homeomorphic to the
 -sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
-sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
- [Penrose&Whitehead&Zeeman1961] R. Penrose, J. Whitehead and E. Zeeman, Imbedding of manifolds in Euclidean space., Ann. of Math. 73 (1961) 613–623. MR0124909 (23 #A2218) Zbl 0113.38101
- [Rourke&Sanderson1972a] C. P. Rourke and B. J. Sanderson, Introduction to piecewise-linear topology, Springer-Verlag, 1972. MR0350744 (50 #3236) Zbl 0477.57003
- [Whitney1944] H. Whitney, The self-intersections of a smooth
 -manifold in
-manifold in  -space, Ann. of Math. (2) 45 (1944), 220–246. MR0010274 (5,273g) Zbl 0063.08237
-space, Ann. of Math. (2) 45 (1944), 220–246. MR0010274 (5,273g) Zbl 0063.08237