Rho-invariant
Tibor Macko (Talk | contribs) |
|||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Introduction == | == Introduction == | ||
<wikitex>; | <wikitex>; | ||
| Line 48: | Line 35: | ||
=== Cobordism theory === | === Cobordism theory === | ||
<wikitex>; | <wikitex>; | ||
| − | For the first one one also needs the result of Conner and Floyd \cite{Conner | + | For the first one one also needs the result of Conner and Floyd \cite{Conner&Floyd1964} and Williamson that for an odd-dimensional manifold $X$ with a finite fundamental group $G$ there always exists a $k \in \Nn$ and a manifold with boundary $(Y,\partial Y)$ such that $\pi_1 (Y) \cong \pi_1 (X) \cong G$ and $\partial Y = k \cdot X$. In other words |
$$ | $$ | ||
\Omega^{\textup{TOP}}_{2d-1} (BG) \otimes \Qq = 0 | \Omega^{\textup{TOP}}_{2d-1} (BG) \otimes \Qq = 0 | ||
Revision as of 09:39, 8 June 2010
Contents |
1 Introduction
The 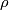 -invariant is an invariant of odd-dimensional closed manifolds closely related to the
equivariant signature. Its definition is motivated by the
equivariant signature defect of even-dimensional manifolds with
boundary. Namely, for manifolds with boundary the classical index
formula for equivariant signature must be corrected by an additional
term. It is this term which gives rise to the
-invariant is an invariant of odd-dimensional closed manifolds closely related to the
equivariant signature. Its definition is motivated by the
equivariant signature defect of even-dimensional manifolds with
boundary. Namely, for manifolds with boundary the classical index
formula for equivariant signature must be corrected by an additional
term. It is this term which gives rise to the 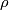 -invariant.
There is also another definition using bordism theory. Finally there
is also an analytic defintion as a relative
-invariant.
There is also another definition using bordism theory. Finally there
is also an analytic defintion as a relative 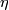 -invariant.
-invariant.
2 Background
2.1 G-index theorem
Let  be a compact Lie group acting smoothly on a smooth manifold
be a compact Lie group acting smoothly on a smooth manifold 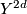 . The middle intersection form becomes a non-degenerate
. The middle intersection form becomes a non-degenerate 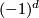 -symmetric bilinear form on which
-symmetric bilinear form on which
 acts. The positivie and negative definite subspaces are
acts. The positivie and negative definite subspaces are  -invariant and hence such a form yields an element in the representation ring
-invariant and hence such a form yields an element in the representation ring 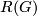 denoted by
denoted by 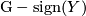 .
In fact
.
In fact 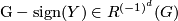 which in terms of characters means that we obtain a real (purely imaginary) character, which will be denoted as
which in terms of characters means that we obtain a real (purely imaginary) character, which will be denoted as
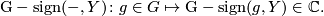
The (cohomological version of the) Atiyah-Singer  -index theorem [Atiyah&Singer1968c, Theorem (6.12)] tells us that if
-index theorem [Atiyah&Singer1968c, Theorem (6.12)] tells us that if  is closed then for all
is closed then for all 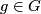
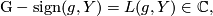
where 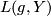 is an expression obtained by evaluating certain cohomological classes on the fundamental classes of the
is an expression obtained by evaluating certain cohomological classes on the fundamental classes of the  -fixed point submanifolds
-fixed point submanifolds 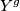 of
of  . In particular if the action is free then
. In particular if the action is free then 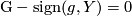 if
if 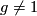 . This means that
. This means that 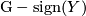 is a multiple of the regular representation. This theorem was generalized by Wall to topological semifree actions on topological manifolds, which is the case we will need in this paper
[Wall1999, chapter 14B].
is a multiple of the regular representation. This theorem was generalized by Wall to topological semifree actions on topological manifolds, which is the case we will need in this paper
[Wall1999, chapter 14B].
The assumption that  is closed is essential, and motivates the definition of the
is closed is essential, and motivates the definition of the 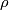 -invariant.
-invariant.
2.2 Cobordism theory
For the first one one also needs the result of Conner and Floyd [Conner&Floyd1964] and Williamson that for an odd-dimensional manifold  with a finite fundamental group
with a finite fundamental group  there always exists a
there always exists a 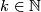 and a manifold with boundary
and a manifold with boundary 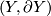 such that
such that 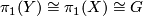 and
and 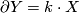 . In other words
. In other words
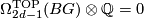
3 Definition
3.1 G finite
Definition 3.1.
Let 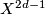 be a closed manifold with
be a closed manifold with 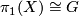 a finite group. Define
a finite group. Define
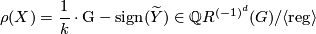
for some 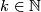 and
and 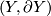 such that
such that 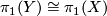 and
and 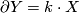 . The symbol
. The symbol 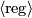 denotes the ideal generated by the regular
representation.
denotes the ideal generated by the regular
representation.
See [Atiyah&Singer1968c, Remark after Corollary 7.5] for more details. Note that the manifold  in the definition always exists by the above mentioned result in cobodism theory. Furthermore the invariant is well-defined thanks to the cohomological version of the
in the definition always exists by the above mentioned result in cobodism theory. Furthermore the invariant is well-defined thanks to the cohomological version of the  -index theorem.
-index theorem.
3.2 G compact Lie group
Definition 3.2 (Atiyah-Singer).
Let  be a compact Lie group acting freely on a manifold
be a compact Lie group acting freely on a manifold 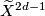 . Suppose in addition that there is a manifold with boundary
. Suppose in addition that there is a manifold with boundary 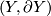 on which
on which  acts (not necessarily freely) and such that
acts (not necessarily freely) and such that 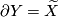 . Define
. Define
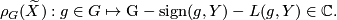
See [Atiyah&Singer1968c, Theorem 7.4] for more details.
In this definition we think about the  -invariant as about a function
-invariant as about a function 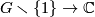 . When both definitions apply (that means when
. When both definitions apply (that means when  is a finite group), then they coincide, that means
is a finite group), then they coincide, that means 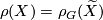 .
.
4 References
- [Atiyah&Singer1968c] Template:Atiyah&Singer1968c
- [Conner&Floyd1964] P. E. Conner and E. E. Floyd, Differentiable periodic maps, Academic Press Inc., Publishers, New York, 1964. MR0176478 (31 #750) Zbl 0417.57019
- [Wall1999] C. T. C. Wall, Surgery on compact manifolds, American Mathematical Society, Providence, RI, 1999. MR1687388 (2000a:57089) Zbl 0935.57003
|
This page has not been refereed. The information given here might be incomplete or provisional. |