Reducible Poincaré Complexes (Ex)
(Difference between revisions)
(Created page with "<wikitex>; {{beginthm|Exercise}} Let $X$ be a finite Poinaré complex of formal dimension $n$ with Spivak Normal Fibration $\nu_X$. A Theorem of {{citeD|Wall1967a|Theorem 2.4...") |
m |
||
| Line 3: | Line 3: | ||
Let $X$ be a finite Poinaré complex of formal dimension $n$ with Spivak Normal Fibration $\nu_X$. A Theorem of {{citeD|Wall1967a|Theorem 2.4}} states that $X$ may be written | Let $X$ be a finite Poinaré complex of formal dimension $n$ with Spivak Normal Fibration $\nu_X$. A Theorem of {{citeD|Wall1967a|Theorem 2.4}} states that $X$ may be written | ||
$$ X \simeq X^\bullet \cup_\phi e^n$$ | $$ X \simeq X^\bullet \cup_\phi e^n$$ | ||
| − | where $X^\bullet$ has dimension less than $n$. Show that for some $k$, the top cell of $X$ splits off, i.e. $\Sigma^k X \simeq S^{n+k} \vee \Sigma^k X^\bullet$, if and only if $\nu_X$ is trivial. | + | where $X^\bullet$ has dimension less than $n$. Show that for some $k$, the top cell of $X$ splits off, i.e. $\Sigma^k X \simeq S^{n+k} \vee \Sigma^k X^\bullet$, if and only if $\nu_X$, the Spivak normal fibration of $X$, is trivial. |
{{endthm}} | {{endthm}} | ||
</wikitex> | </wikitex> | ||
Revision as of 23:34, 27 August 2013
Exercise 0.1.
Let  be a finite Poinaré complex of formal dimension
be a finite Poinaré complex of formal dimension  with Spivak Normal Fibration
with Spivak Normal Fibration 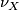 . A Theorem of [Wall1967a, Theorem 2.4] states that
. A Theorem of [Wall1967a, Theorem 2.4] states that  may be written
may be written
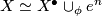
where 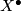 has dimension less than
has dimension less than  . Show that for some
. Show that for some  , the top cell of
, the top cell of  splits off, i.e.
splits off, i.e. 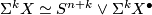 , if and only if
, if and only if 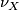 , the Spivak normal fibration of
, the Spivak normal fibration of  , is trivial.
, is trivial.